【题目】如图,矩形ABCD中,点E、F、G. H分别AB、BC、 CD、 DA边上的动点,且AE=BF=CG=DH

(1)求证:四边形EFGH是平行四边形:
(2)在点E、F、G、H运动过程中,判断直线GE是否经过某一定点,如果是,请你在图中画出这个点:如果不是,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)是,直线GE总过AC、BD的交点M,作图见解析.
【解析】
(1)由矩形的性质得出∠A=∠C=90°,BC=AD,由AE=BF=CG=DH证出AH=CF,由SAS证明△AEH≌△CGF,可得HE=FG,同理可得HG=FE即可求解;
(2)直线GE经过一个定点,这个定点为矩形的对角线AC、BD的交点.只要证明四边形AECG是平行四边形,即可推出MA=MG,MG=ME,即点M为AC的中点,又矩形ABCD的对角线互相平分,推出点M为矩形对角线ACBD的交点.
解:(1)∵四边形ABCD为矩形,
∴BC=AD,∠A=∠C=90°,
∵BF=DH,
∴BC-BF=AD-DH,即CF=AH,
又AE=CG,
∴△HAE≌△FCG,
∴HE=FG,
同理可证:HG=FE,
∴四边形EFGH是平行四边形.
(2)直线GE经过一个定点,这个定点为矩形的对角线AC、BD的交点.
理由如下:
如图,连结AC、AG、CE,设AC、EG的交点为M.
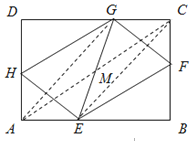
∵AE∥CG,AE=CG,
∴四边形AECG是平行四边形,
∴MA=MG,MG=ME,
即点M为AC的中点,
又矩形ABCD的对角线互相平分
∴点M为矩形对角线ACBD的交点,
∴直线GE总过AC、BD的交点M.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要从甲、乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.

(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接指出甲,乙这10次射击成绩的方差s甲2,s乙2哪个大?
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选哪位参赛更合适?为什么?如果其他班级参赛选手的射击成绩都在9环左右,本班应该选哪位参赛更合适?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
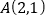 ,
,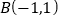 ,
,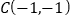 ,
,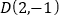 ,把一根长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在
,把一根长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在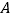 处,并按
处,并按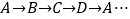 的规律紧绕在四边形
的规律紧绕在四边形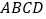 的边上,则细线的另一端点所在位置的坐标是__________.
的边上,则细线的另一端点所在位置的坐标是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校美术组要购买铅笔和橡皮,按照商店规定,若同时购买60支铅笔和30块橡皮,则需按零售价购买,共需支付30元;若同时购买90支铅笔和60块橡皮,则可按批发价购买,共需支付40.5元.已知每支铅笔的批发价比零售价低0.05元,每块橡皮的批发价比零售价低0.10元.求每支铅笔和每块橡皮的批发价各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
某些代数恒等式可用一些卡片拼成的图形的面积来解释.例如,图①可以解释
 ,因此,我们可以利用这种方法对某些多项式进行因式分解.
,因此,我们可以利用这种方法对某些多项式进行因式分解.
根据阅读材料回答下列问题:
(1)如图②所表示的因式分解的恒等式是________________________.
(2)现有足够多的正方形和长方形卡片(如图③),试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的长方形(每两张卡片之间既不重叠,也无空隙),使该长方形的面积为
 ,并利用你画的长方形的面积对
,并利用你画的长方形的面积对 进行因式分解.
进行因式分解. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,点
,点 ,
, 分别是边
分别是边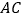 ,
, 上的点,点
上的点,点 是一动点.记
是一动点.记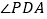 为
为 ,
, 为
为 ,
, 为
为 .
.
(1)若点
 在线段
在线段 上,且
上,且 ,如图1,则
,如图1,则 _____________;
_____________;(2)若点
 在边
在边 上运动,如图2所示,请猜想
上运动,如图2所示,请猜想 ,
, ,
, 之间的关系,并说明理由;
之间的关系,并说明理由;(3)若点
 运动到边
运动到边 的延长线上,如图3所示,则
的延长线上,如图3所示,则 ,
, ,
, 之间又有何关系?请直接写出结论,不用说明理由.
之间又有何关系?请直接写出结论,不用说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人站成一横排照相,因甲、乙两人是好友,照相时两人紧邻着站在一起不分开.
(1)请按左、中、右的顺序列出所有符合要求的站位的结果;
(2)按要求随机的站立,求丙站在甲左边的概率.
相关试题

