【题目】如图,在平面直角坐标系中,直线y=﹣![]() x﹣
x﹣![]() 交x轴于点A,交y轴于点C,直线y=
交x轴于点A,交y轴于点C,直线y=![]() x﹣5
x﹣5![]() 交x轴于点B,在平面内有一点E,其坐标为(4,
交x轴于点B,在平面内有一点E,其坐标为(4,![]() ),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移
),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
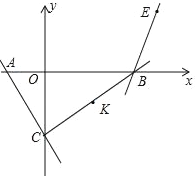
参考答案:
【答案】![]()
【解析】
由解析式求出A、B、C点坐标,进而求得K的坐标,关键平移的规律求得K′的坐标,将K′向右平移1个单位得到H,作H关于x轴的对称点H′,连接EH′交x轴于N,此时四边形K′MNE的周长最小.求出直线EH′的解析式即可解决问题.
∵直线y=﹣![]() x﹣
x﹣![]() 交x轴于点A,交y轴于点C,直线y=
交x轴于点A,交y轴于点C,直线y=![]() x﹣5
x﹣5![]() 交x轴于点B,
交x轴于点B,
∴A(﹣1,0),
∴B(3,0),C(0,﹣![]() ),
),
∵K是BC中点,
∴k(![]() ,﹣
,﹣![]() ),
),
∵将K点先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位得K′,
个单位得K′,
∴K′(1,![]() ),
),
如图,将K′向右平移1个单位得到H,作H关于x轴的对称点H′,连接EH′交x轴于N,此时四边形K′MNE的周长最小.
∵H(2,![]() ),H′(2,﹣
),H′(2,﹣![]() ),
),
∴直线EH′的解析式为y=![]() x﹣
x﹣![]() ,
,
令y=0,得到x=![]() ,
,
∴N(![]() ,0),
,0),
∴a=![]() ﹣1=
﹣1=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1⊥x轴于点A(2,0),点B是直线l1上的动点.直线l2:y=x+1交l1于点C,过点B作直线l3垂直于l2 , 垂足为D,过点O,B的直线l4交l2于点E,当直线l1 , l2 , l3能围成三角形时,设该三角形面积为S1 , 当直线l2 , l3 , l4能围成三角形时,设该三角形面积为S2 .

(1)若点B在线段AC上,且S1=S2 , 则B点坐标为;
(2)若点B在直线l1上,且S2= S1 , 则∠BOA的度数为 .
S1 , 则∠BOA的度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形,
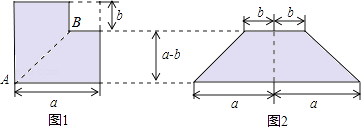
(1)设图1中阴影部分面积为S1 , 图2中阴影部分面积为S2 , 请直接用含a、b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在义乌市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为:“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.

请你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.

(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA=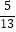 ,求EF的长.
,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件)
1
2
…
A产品单价(元/件)
1480
1460
…
B产品单价(元/件)
1290
1280
…
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,后解答:
(1)由根式的性质计算下列式子得:
①
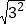 =3,②
=3,②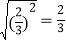 ,③
,③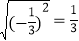 ,④
,④ =5,⑤
=5,⑤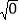 =0.
=0.由上述计算,请写出
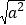 的结果(a为任意实数).
的结果(a为任意实数).(2)利用(1)中的结论,计算下列问题的结果:
①
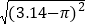 ;
;②化简:
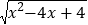 (x<2).
(x<2).(3)应用:
若
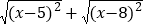 =3,求x的取值范围.
=3,求x的取值范围.
相关试题

