【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为|AB|=|a﹣b|.
![]()
根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、﹣1,
①A、B之间的距离可用含x的式子表示为 ;
②若该两点之间的距离为2,那么x值为 .
(2)|x+1|+|x﹣2|的最小值为 ,此时x的取值是 ;
(3)已知(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15,求x﹣2y的最大值 和最小值 .
参考答案:
【答案】(1)①|x+1|;②﹣3或1;(2)3,﹣1≤x≤2;(3)6,﹣7.
【解析】试题分析:(1)①根据题目已知中的 A、B 两点间的距离表示为|AB|=|a﹣b|.即可解答;②使①中的式子等于 2,解出即可;(2)求|x+1|+|x﹣2|的最小值,由线段的性质,两点之间,线段最短,可知当﹣1≤x≤2 时,|x+1|+|x﹣2|有最小值,再根据绝对值的性质即可求出最小值及x 的取值;(3)由于(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15=3×5,可知﹣1≤x≤2,﹣2≤y≤3,依此得到 x﹣2y 的最大值和最小值.
试题解析:
(1)①A、B 之间的距离可用含 x 的式子表示为|x+1|;
②依题意有|x+1|=2,所以x+1=﹣2 或 x+1=2, 解得 x=﹣3 或 x=1.
(2)|x+1|+|x﹣2|的最小值为 3,此时 x 的取值是﹣1≤x≤2;
(3)∵(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15,
∴﹣1≤x≤2,﹣2≤y≤3,
∴x﹣2y 的最大值为 2﹣2×(﹣2)=6,最小值为﹣1﹣2×3=﹣7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|=|a﹣b|.
理解:
(1)数轴上表示2和﹣3的两点之间的距离是 ;
(2)数轴上表示x和﹣5的两点A和B之间的距离是 ;
(3)当代数式|x﹣1|+|x+3|取最小值时,相应的x的取值范围是 ;最小值是 .
应用:某环形道路上顺次排列有四家快递公司:A、B、C、D,它们顺次有快递车16辆,8辆,4辆,12辆,为使各快递公司的车辆数相同,允许一些快递公司向相邻公司调出,问共有多少种调配方案,使调动的车辆数最少?并求出调出的最少车辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a-b+c的相反数是
A. –a-b-c B. –a+b-c C. -a-b+c D. a+b-c
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列是勾股数的一组是( )
A.4,5,6B.5,7,12C.12,13,15D.21,28,35
-
科目: 来源: 题型:
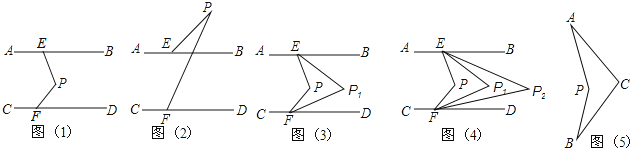
查看答案和解析>>【题目】如图(1),直线AB∥CD,点P在两平行线之间,点E在AB上,点F在CD上,连结PE,PF.
(1)∠PEB,∠PFD,∠EPF满足的数量关系是 ,并说明理由.
(2)如图(2),若点P在直线AB上侧时,∠PEB,∠PFD,∠EPF满足的数量关系是 (不需说明理由)
(3)如图(3),在图(1)基础上,P
 E平分∠PEB,P
E平分∠PEB,P F平分∠PFD,若设∠PEB=x°,∠PFD=y°.则∠P
F平分∠PFD,若设∠PEB=x°,∠PFD=y°.则∠P =______(用x,y的代数式表示),若P
=______(用x,y的代数式表示),若P E平分∠P
E平分∠P EB,P
EB,P F平分∠P
F平分∠P FD,可得∠P
FD,可得∠P ,P
,P E平分∠P
E平分∠P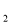 EB,P
EB,P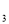 F平分∠P
F平分∠P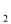 FD,可得∠P
FD,可得∠P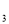 …,依次平分下去,则∠P
…,依次平分下去,则∠P =______.
=______.(4)科技活动课上,雨轩同学制作了一个图(5)的“飞旋镖”,经测量发现∠PAC=28°,
∠PBC=30°,他很想知道∠APB与∠ACB的数量关系,你能告诉他吗?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=kx(k≠0)经过点(-2,6),则y随x的增大而
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2向左平移1个单位,再向下平移3个单位,则平移后的抛物线的解析式为( )
A.y=2(x+1)2+3
B.y=2(x+1)2﹣3
C.y=2(x﹣1)2﹣3
D.y=2(x﹣1)2+3
相关试题

