【题目】阅读:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|=|a﹣b|.
理解:
(1)数轴上表示2和﹣3的两点之间的距离是 ;
(2)数轴上表示x和﹣5的两点A和B之间的距离是 ;
(3)当代数式|x﹣1|+|x+3|取最小值时,相应的x的取值范围是 ;最小值是 .
应用:某环形道路上顺次排列有四家快递公司:A、B、C、D,它们顺次有快递车16辆,8辆,4辆,12辆,为使各快递公司的车辆数相同,允许一些快递公司向相邻公司调出,问共有多少种调配方案,使调动的车辆数最少?并求出调出的最少车辆.
参考答案:
【答案】(1)5;(2)|x+5|;(3)﹣3≤x≤1,4;应用:方案见解析,12辆.
【解析】试题分析:根据题意,可以求得第(1),(2),(3)的答案,根据应用的题意,可以画出五种调配方案,从而可以解答本题.
试题解析:
(1)2 和﹣3 的两点之间的距离是|2﹣(﹣3)|=5.
(2)A 和 B 之间的距离是|x﹣(﹣5)|=|x+5|.
(3)代数式|x﹣1|+|x+3|表示在数轴上到 1 和﹣3 两点的距离的和,当 x 在﹣3 和 1 之间时,代数式取得最小值,最小值是﹣3 和 1 之间的距离|1﹣(﹣3)|=4. 故当﹣3≤x≤1 时,代数式取得最小值,最小值是 4.
应用:根据题意,共有 5 种调配方案,如下图所示:




由上可知,调出的最小车辆数为:4+2+6=12 辆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a,b在数轴上的位置如图所示.
(1)在数轴上标出﹣a,﹣b的位置,并比较a,b,﹣a,﹣b的大小:
(2)化简|a+b|+|a﹣b|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将2.9,1.9,0,3.9这四个数在数轴上表示出来,排在最左边的数是( )
A. 0 B. -1.9 - C. -2.9 D. -3.9
-
科目: 来源: 题型:
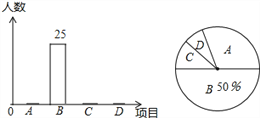
查看答案和解析>>【题目】某校的20年校庆举办了四个项目的比赛,现分别以A,B,C,D表示它们.要求每位同学必须参加且限报一项.以701班为样本进行统计,并将统计结果绘制如下两幅统计图,其中参加A项目的人数比参加C与D项目人数的总和多1人,参加D项目的人数比参加A项目的人数少11人.请你结合图中所给出的信息解答下列问题:
(1)求出全班总人数;
(2)求出扇形统计图中参加D项目比赛的学生所在的扇形圆心角的度数;
(3)若该校7年级学生共有200人,请你估计这次活动中参加A和B项目的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】a-b+c的相反数是
A. –a-b-c B. –a+b-c C. -a-b+c D. a+b-c
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列是勾股数的一组是( )
A.4,5,6B.5,7,12C.12,13,15D.21,28,35
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为|AB|=|a﹣b|.

根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、﹣1,
①A、B之间的距离可用含x的式子表示为 ;
②若该两点之间的距离为2,那么x值为 .
(2)|x+1|+|x﹣2|的最小值为 ,此时x的取值是 ;
(3)已知(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15,求x﹣2y的最大值 和最小值 .
相关试题

