【题目】如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题.
(1)画出△ABC的高AD;
(2)画出△ABC的角平分线AE;
(3)根据你所画的图形求∠DAE的度数.

参考答案:
【答案】(1)详见解析;(2)详见解析;(3)35°.
【解析】
(1)过A点作BC延长线的垂线即可得到高AD;(2)根据角平分线的尺规作图即可作图;(3)先根据三角形的内角和求出∠CAB,再求出∠EAB,再根据三角形的外角定理求出∠AED,最后根据直角三角形求出∠DAE的度数.
(1)如图,AD即为所求作的高;

(2)如图,AE即为所求作的角平分线;
(3)在△ABC中,∵∠B=40°,∠C=110°,
∴∠CAB=180°-40°-110°=30°,
∵AE平分∠CAB,
∴∠EAB=![]() ∠CAB=15°,
∠CAB=15°,
∵∠AED是△ABE的外角,
∴∠AED=∠B+∠EAB=55°,
∵AD⊥BC,
∴∠ADB=90°,
∴在Rt△ADE中,∠DAE=90°-∠AED=90°-55°=35°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,存在直线
 和直线
和直线 .
.(1)直接写出
 两点的坐标;
两点的坐标; (2)求出直线
 、直线
、直线 的交点
的交点 及两条直线与
及两条直线与 轴围成的三角形的面积;
轴围成的三角形的面积;(3)结合图象,直接写出
 时
时 的取值范围_______.
的取值范围_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:
(概念理解)
在一个三角形中,如果一个角的度数是另一个角度数的 4 倍,那么这样的三角形我们称之为“完美三角形”.如:三个内角分别为 130°,40°,10°的三角形是“完美三角形”.
(简单应用)
如图 1,∠MON=72°,在射线OM上找一点A,过点A作AB⊥OM 交ON于点B,以A为端点作射线AD,交线段OB 于点C(点 C不与 O,B重合)
(1)∠ABO= ,△AOB__________(填“是”或“不是”)“完美三角形”;
(2)若∠ACB=90°,求证:△AOC是“完美三角形”.
(应用拓展)
如图 2,点D在△ABC 的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使
 ,
, .若△BCD是“完美三角形”, 求∠B的度数.
.若△BCD是“完美三角形”, 求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.

(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2 ,求阴影部分的面积.
,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 分别为边
分别为边 的中点,
的中点, 是对角线,过点
是对角线,过点 作
作 交
交 的延长线于点
的延长线于点 .
.(1)求证:
 ;
;(2)若
 ,求证:四边形
,求证:四边形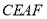 是菱形.
是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校利用五一组织老师去娄山关进行红色文化拓展活动,现有甲、乙两家旅行 社可供选择,票价都是
 元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前
元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前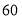 人按原价付费,超过的部分
人按原价付费,超过的部分 折优惠.该校有教师
折优惠.该校有教师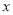 人.
人. (1)设总价为
 元.写出
元.写出 与
与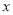 之间的函数关系式;
之间的函数关系式; (2)在不晓得该校人数的情况下,请给学校提出比较省钱的购票建议.
相关试题

