【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2 ![]() ,求阴影部分的面积.
,求阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OC,如图,
∵CE为切线,
∴OC⊥CE,
∴∠OCE=90°,
∵OD⊥BC,
∴CD=BD,
即OD垂中平分BC,
∴EC=EB,
在△OCE和△OBE中
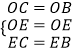 ,
,
∴△OCE≌△OBE,
∴∠OBE=∠OCE=90°,
∴OB⊥BE,
∴BE与⊙O相切
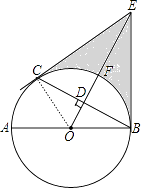
(2)解:设⊙O的半径为r,则OD=r﹣1,
在Rt△OBD中,BD=CD= ![]() BC=
BC= ![]() ,
,
∴(r﹣1)2+( ![]() )2=r2,解得r=2,
)2=r2,解得r=2,
∵tan∠BOD= ![]() =
= ![]() ,
,
∴∠BOD=60°,
∴∠BOC=2∠BOD=120°,
在Rt△OBE中,BE= ![]() OB=2
OB=2 ![]() ,
,
∴阴影部分的面积=S四边形OBEC﹣S扇形BOC
=2S△OBE﹣S扇形BOC
=2× ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]()
=4 ![]() ﹣
﹣ ![]() π
π
【解析】(1)连接OC,如图,利用切线的性质得∠OCE=90°,再根据垂径定理得到CD=BD,则OD垂中平分BC,所以EC=EB,接着证明△OCE≌△OBE得到∠OBE=∠OCE=90°,然后根据切线的判定定理得到结论;(2)设⊙O的半径为r,则OD=r﹣1,利用勾股定理得到(r﹣1)2+( ![]() )2=r2 , 解得r=2,再利用三角函数得到∠BOD=60°,则∠BOC=2∠BOD=120°,接着计算出BE=
)2=r2 , 解得r=2,再利用三角函数得到∠BOD=60°,则∠BOC=2∠BOD=120°,接着计算出BE= ![]() OB=2
OB=2 ![]() , 然后根据三角形面积公式和扇形的面积公式,利用阴影部分的面积=2S△OBE﹣S扇形BOC进行计算即可.
, 然后根据三角形面积公式和扇形的面积公式,利用阴影部分的面积=2S△OBE﹣S扇形BOC进行计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:
(概念理解)
在一个三角形中,如果一个角的度数是另一个角度数的 4 倍,那么这样的三角形我们称之为“完美三角形”.如:三个内角分别为 130°,40°,10°的三角形是“完美三角形”.
(简单应用)
如图 1,∠MON=72°,在射线OM上找一点A,过点A作AB⊥OM 交ON于点B,以A为端点作射线AD,交线段OB 于点C(点 C不与 O,B重合)
(1)∠ABO= ,△AOB__________(填“是”或“不是”)“完美三角形”;
(2)若∠ACB=90°,求证:△AOC是“完美三角形”.
(应用拓展)
如图 2,点D在△ABC 的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC上取点F,使
 ,
, .若△BCD是“完美三角形”, 求∠B的度数.
.若△BCD是“完美三角形”, 求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=110°.按要求完成下列各题.
(1)画出△ABC的高AD;
(2)画出△ABC的角平分线AE;
(3)根据你所画的图形求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 分别为边
分别为边 的中点,
的中点, 是对角线,过点
是对角线,过点 作
作 交
交 的延长线于点
的延长线于点 .
.(1)求证:
 ;
;(2)若
 ,求证:四边形
,求证:四边形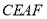 是菱形.
是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校利用五一组织老师去娄山关进行红色文化拓展活动,现有甲、乙两家旅行 社可供选择,票价都是
 元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前
元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前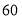 人按原价付费,超过的部分
人按原价付费,超过的部分 折优惠.该校有教师
折优惠.该校有教师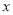 人.
人. (1)设总价为
 元.写出
元.写出 与
与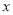 之间的函数关系式;
之间的函数关系式; (2)在不晓得该校人数的情况下,请给学校提出比较省钱的购票建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象分别与
的图象分别与 轴,
轴, 轴交于
轴交于 ,以线段
,以线段 为边在第一象限内作等腰直角三角形
为边在第一象限内作等腰直角三角形 ,使
,使 .
.(1)分别求点
 的坐标;
的坐标; (2)在
 轴上求一点
轴上求一点 ,使它到
,使它到 两点的距离之和最小.
两点的距离之和最小.
相关试题

