【题目】将正整数按如图的规律排列:平移表中的方框,方框中的4个数的和可能是( )
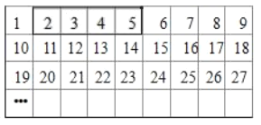
A.2010B.2014C.2018D.2022
参考答案:
【答案】A
【解析】
设第二个为x,则第一个,第三个,第四个分别为:x-1,x+1,x+2,总和为:4x+2,分别令代数式为:2010,2014,2018,2022,算出x再判断.
解: 设第二个为x,则第一个,第三个,第四个分别为:x-1,x+1,x+2,总和为:4x+2.
当4x+2=2010时,x=502,则x-1=501;
当4x+2=2014时,x=503,则x-1=502;
当4x+2=2018时,x=504,则x-1=503;
当4x+2=2022时,x=505,则x-1=504;
由图可知每行有9个数,
∵504÷9=56,可以除尽
故504为某行的最后一位.表格如下:
496 | 497 | 498 | 499 | 500 | 501 | 502 | 503 | 504 |
505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 |
由图可知:501+502+503+504=2010满足题意.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料并回答问题
观察:有理数-2和-4在数轴上对应的两点之间的距离是
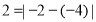 ,有理数1和-3在数轴上对应的两点之间的距离是
,有理数1和-3在数轴上对应的两点之间的距离是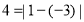

归纳:有理数a、b在数轴上对应的两点A.B之间的距离是
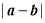 ,反之,
,反之,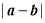 表示有理数a、b在数轴上对应点A.B之间的距离,称之为绝对值的几何意义
表示有理数a、b在数轴上对应点A.B之间的距离,称之为绝对值的几何意义应用:
(1)如果表示-1的点A和表示x点B之间的距离是2,那么x为________;
(2)方程
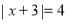 的解为________;
的解为________;(3)小松同学在解方程
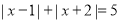 时,利用绝对值的几何意义分析得到,该方程的左边表示在数轴上x对应点到1和-2对应点的距离之和,而当
时,利用绝对值的几何意义分析得到,该方程的左边表示在数轴上x对应点到1和-2对应点的距离之和,而当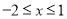 时,取到它的最小值3,即为1和-2对应的点的距离.由方程右边的值为5可知,满足方程的x对应点在1的右边或-2的左边,若x的对应点在1的右边,利用数轴分析可以看出
时,取到它的最小值3,即为1和-2对应的点的距离.由方程右边的值为5可知,满足方程的x对应点在1的右边或-2的左边,若x的对应点在1的右边,利用数轴分析可以看出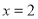 ;同理,若x的对应点在-2的左边,可得
;同理,若x的对应点在-2的左边,可得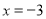 ;故原方程的解是
;故原方程的解是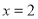 或
或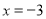 ;参考小松的解答过程,求方程
;参考小松的解答过程,求方程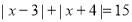 的解.
的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=45°,∠BCA=30°,点D在BC上,点E在△ABC外,且AD=AE=CE,AD⊥AE,则
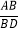 的值为____________.
的值为____________.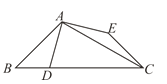
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上
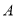 点表示数
点表示数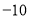 ,
,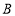 点表示数6,
点表示数6,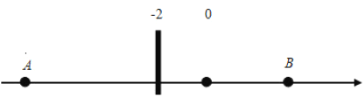
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点
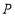 ,它表示的数是
,它表示的数是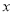 ,则
,则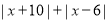 的最小值是_________;
的最小值是_________;(3)若点
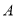 与点
与点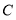 之间的距离表示为
之间的距离表示为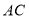 ,点
,点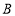 与点
与点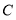 之间的距离表示为
之间的距离表示为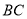 ,请在数轴上找一点
,请在数轴上找一点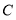 ,使
,使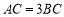 ,则
,则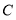 点表示的数是_________;
点表示的数是_________;(4)若在原点
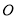 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点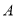 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点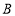 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为 秒,请用
秒,请用 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离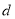 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1,l2,l3分别过正方形ABCD的三个顶点A,D,C,且相互平行,若l1,l2的距离为2,l2,l3的距离为4,则正方形的对角线长为_______________.
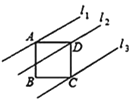
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=
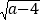 +
+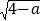 -1.
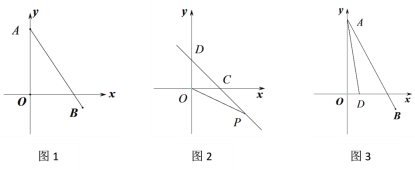
-1.(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形
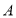 的边长是1米;
的边长是1米;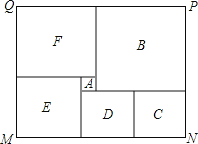
(1)若设图中最大正方形
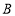 的边长是
的边长是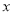 米,请用含
米,请用含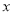 的代数式分别表示出正方形
的代数式分别表示出正方形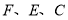 的边长
的边长(2)观察图形的特点可知,长方形相对的两边是相等的(即
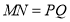 ,
, 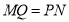 )请根据以上结论,求出
)请根据以上结论,求出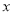 的值
的值(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
相关试题

