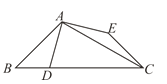
【题目】如图,△ABC中,∠ABC=45°,∠BCA=30°,点D在BC上,点E在△ABC外,且AD=AE=CE,AD⊥AE,则![]() 的值为____________.
的值为____________.
参考答案:
【答案】![]()
【解析】
过A点作BC的垂线,E点作AC的垂线,构造全等三角形,利用对应角相等计算得出∠DAM=15°,在AM上截取AG=DG,则∠DGM=30°,设DM=a,通过勾股定理可得到DG=AG=2a,GM=![]() a,AM=BM=(
a,AM=BM=(![]() ,BD=(
,BD=(![]() ,AB=
,AB=![]() (
(![]() ,代入计算即可.
,代入计算即可.
过A点作AM⊥BC于M点,过E点EN⊥AC于N点.
∵∠BCA=30°,AE=EC
∴AM=![]() AC,AN=
AC,AN=![]() AC
AC
∴AM=AN
又∵AD=AE
∴RtADM RtAEN(HL)
∴∠DAM=∠EAN
又∵∠MAC=60°,AD⊥AE
∴∠DAM=∠EAN=15°
在AM上截取AG=DG,则∠DGM=30°
设DM=a,则 DG=AG=2a,
根据勾股定理得:GM=![]() a,
a,
∵∠ABC=45°
∴AM=BM=(![]()
∴BD=(![]() ,AB=
,AB=![]() (
(![]() ,
,
∴![]()
故答案为:![]()

-
科目: 来源: 题型:
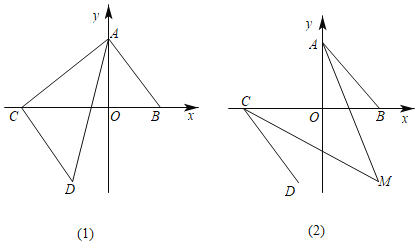
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A(0,4),B(3,0),线段AB平移后对应的线段为CD,点C在x轴的负半轴上,B、C两点之间的距离为8.
(1)求点D的坐标;
(2)如图(1),求△ACD的面积;
(3)如图(2),∠OAB与∠OCD的角平分线相交于点M,探求∠AMC的度数并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:(1)
 ;(2)
;(2) ;(3)
;(3) ;(4)
;(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种汽车可装油400L,若汽车每小时的用油量为x(L).(1)用油量y(h)与每小时的用油量x(L)的函数关系式为______________;(2)若每小时的用油量为20L,则这些油可用的时间为______________;(3)若要使汽车继续行驶40h不需供油,则每小时用油量的范围是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数
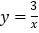 ,
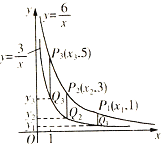
, 在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数
在第一象限内的图象如图所示,点P1,P2,P3,……P2005在反比例函数 图象上,它们的横坐标分别是x1,x2,x3,x2005纵坐标分别为1,3,5,……;
图象上,它们的横坐标分别是x1,x2,x3,x2005纵坐标分别为1,3,5,……;共2005个连续奇数,过点P1,P2,P3,……,P2005分别作
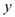 轴的平行线,与
轴的平行线,与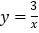 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2005(x2005,y2005),则
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2005(x2005,y2005),则 _____________.
_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
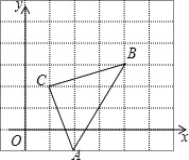
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ 、 )
(4)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 (2)
(2) .
.(3)-27+(-32)+(-8)+72 (4)
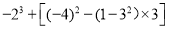
相关试题

