【题目】如图,![]() 的三个顶点的坐标分别是
的三个顶点的坐标分别是![]() ,将
,将![]() 先向右平移
先向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度得到
个单位长度得到![]() .
.

(1)在平面直角坐标系中,画出平移后的![]() ;
;
(2)求出![]() 的面积;
的面积;
(3)点![]() 是
是![]() 轴上的一点,若
轴上的一点,若![]() 的面积等于
的面积等于![]() 的面积,求点
的面积,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据点的平移规律确定平移后点的坐标,再将所得点顺次连接即可解答;
(2)用割补法求解可得答案;
(3)由(2)可知![]() 的面积是
的面积是![]() ,所以
,所以![]() 的面积也是
的面积也是![]() ,因为
,因为![]() 都在x轴上,所以直接以
都在x轴上,所以直接以![]() 为底可得
为底可得![]() 的长为5,再分P在A1的左侧和右侧两种情况讨论即可求出P的坐标.
的长为5,再分P在A1的左侧和右侧两种情况讨论即可求出P的坐标.
解:∵![]() 向右平移
向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度,
个单位长度,
![]() ,
,
将这三个点描出并依次连接得到答案如图:
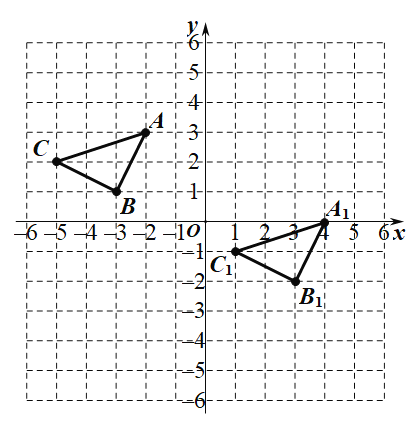 ;
;
(2)用割补法可得:![]() ;
;
(3)由(2)可知![]() 的面积是
的面积是![]() ,
,
∴![]() 的面积也是
的面积也是![]() ,
,
∵![]() 都在x轴上,
都在x轴上,
![]() ,
,
解得![]() ,
,
∵![]() ,
,
![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了增强学生的身体素质,西南大学附中七年级学生在每天晚自习之后进行夜跑.在学期末的体育考试中,七年级的同学们表现出很好的体育素养,并取得了良好的体育成绩.为了了解七年级学生的体育考试情况,小明抽取了部分同学的体育考试成绩进行分析,体育成绩优、良、中、差分别记为
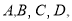 并绘制了如下两幅不完整的统计表:
并绘制了如下两幅不完整的统计表:
(1)本次调查共调查了 名学生,并补全条形统计图;
(2)扇形统计图中
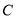 类所对应的扇形圆心角的度数是 度;
类所对应的扇形圆心角的度数是 度;(3)若七年级人数为
 人,请你估计体育成绩优、良的总人数.
人,请你估计体育成绩优、良的总人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点P(1,﹣4)、Q(m,n)在函数
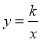 (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )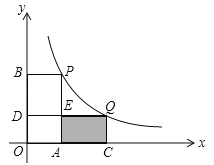
A.减小 B.增大 C.先减小后增大 D.先增大后减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y1=a(x﹣2)2+k中,函数y1与自变量x的部分对应值如表:
x
…
1
2
3
4
…
y
…
2
1
2
5
…
(1)求该二次函数的表达式; -
科目: 来源: 题型:
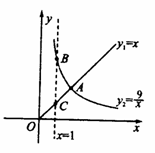
查看答案和解析>>【题目】函数 yl= x ( x ≥0 ) ,
 ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3  时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .
-
科目: 来源: 题型:
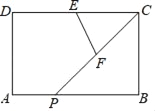
查看答案和解析>>【题目】如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题探究】
已知:如图①所示,∠MPN的顶点为P,⊙O的圆心O从顶点P出发,沿着PN方向平移.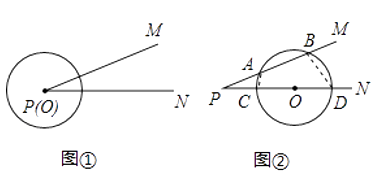
(1)如图②所示,当⊙O分别与射线PM,PN相交于A、B、C、D四个点,连接AC、BD,可以证得△PAC∽△ , 从而可以得到:PAP B=P CP D.
(2)如图③所示,当⊙O与射线PM相切于点A,与射线PN相交于C、D两个点.求证:PA2=PCPD.
(3)【简单应用】
如图④所示,(2)中条件不变,经过点P的另一条射线与⊙O相交于E、F两点.利用上述(1),(2)两问的结论,直接写出线段PA与PE、PF之间的数量关系;当PA=4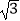 ,EF=2,则PE= .
,EF=2,则PE= . 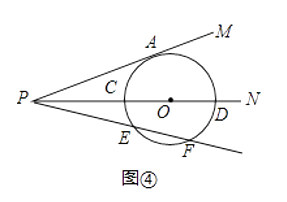
(4)【拓展延伸】如图⑤所示,在以O为圆心的两个同心圆中,A、B是大⊙O上的任意两点,经过A、B 两点作线段,分别交小⊙O于C、E、D、F四个点.求证:ACAE=BDBF.(友情提醒:可直接运用本题上面所得到的相关结论)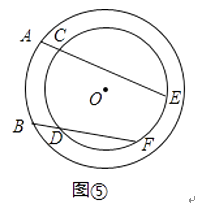
相关试题

