【题目】【问题探究】
已知:如图①所示,∠MPN的顶点为P,⊙O的圆心O从顶点P出发,沿着PN方向平移.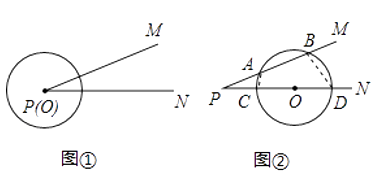
(1)如图②所示,当⊙O分别与射线PM,PN相交于A、B、C、D四个点,连接AC、BD,可以证得△PAC∽△ , 从而可以得到:PAP B=P CP D.
(2)如图③所示,当⊙O与射线PM相切于点A,与射线PN相交于C、D两个点.求证:PA2=PCPD.
(3)【简单应用】
如图④所示,(2)中条件不变,经过点P的另一条射线与⊙O相交于E、F两点.利用上述(1),(2)两问的结论,直接写出线段PA与PE、PF之间的数量关系;当PA=4 ![]() ,EF=2,则PE= .
,EF=2,则PE= . 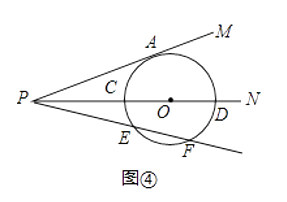
(4)【拓展延伸】如图⑤所示,在以O为圆心的两个同心圆中,A、B是大⊙O上的任意两点,经过A、B 两点作线段,分别交小⊙O于C、E、D、F四个点.求证:ACAE=BDBF.(友情提醒:可直接运用本题上面所得到的相关结论)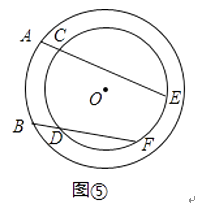
参考答案:
【答案】
(1)△PDB
(2)证明:连接AC、AD,如图③所示:
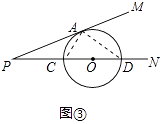
∵⊙O与射线PM相切于点A,与射线PN相交于C、D两个点,
∴∠PAC=∠PDA,
又∵∠P=∠P,
∴△PAC∽△PDA,
∴PA:PD=PC:PA,
∴PA2=PCPD
(3)PA2=PE?PF,6
(4)证明:过A作⊙O的切线AM,M为切点,过B作⊙O的切线BN,N为切点,连接OA、OM、OB、ON,则AM⊥OM,BN⊥ON,如图⑤所示:
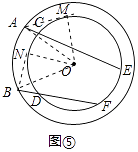
由(3)得:AM2=ACAE,BN2=BDBF.
在Rt△AOM中,AM2=OA2﹣OM2,
在Rt△BON中,BN2=OB2﹣ON2,
又∵OM=ON,OA=OB,
∴AM2=BN2,
∴ACAE=BDBF.
【解析】(1)解:由圆内接四边形的性质得:∠PAC=∠PDB,
又∵∠P=∠P,
∴△PAC∽△PDB,
∴PA:PD=PC:PB,
∴PAP B=P CP D.
所以答案是:△PDB;(3)解:由(2)得:PA2=PEPF.
∵PA=4 ![]() ,EF=2,
,EF=2,
∴PEPF=(4 ![]() )2=48,
)2=48,
即PE(PE+2)=48,
解得:PE=6,或PE=﹣8(舍去),
∴PE=6,
所以答案是:PA2=PEPF,6;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 的三个顶点的坐标分别是
的三个顶点的坐标分别是 ,将
,将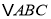 先向右平移
先向右平移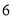 个单位长度,再向下平移
个单位长度,再向下平移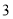 个单位长度得到
个单位长度得到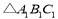 .
.
(1)在平面直角坐标系中,画出平移后的
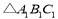 ;
;(2)求出
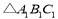 的面积;
的面积;(3)点
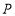 是
是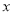 轴上的一点,若
轴上的一点,若 的面积等于
的面积等于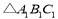 的面积,求点
的面积,求点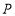 的坐标.
的坐标. -
科目: 来源: 题型:
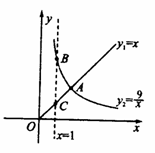
查看答案和解析>>【题目】函数 yl= x ( x ≥0 ) ,
 ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3  时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .
-
科目: 来源: 题型:
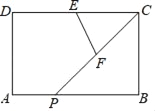
查看答案和解析>>【题目】如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 直线
直线 分别交
分别交 于点
于点 与
与 的角平分线交于点
的角平分线交于点 与
与 交于点
交于点 交
交 于
于 .
.
(1)求证:
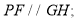
(2)如图2,连接
 为
为 上一动点,
上一动点, 平分
平分 交
交 于
于 则
则 的大小是否发生变化?若不变,求出其值;若改变,请说明理由.
的大小是否发生变化?若不变,求出其值;若改变,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=﹣
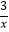 ,下列结论不正确的是( )
,下列结论不正确的是( )
A.图象必经过点(﹣1,3)
B.若x>1,则﹣3<y<0
C.图象在第二、四象限内
D.y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OACB的顶点O在原点,点C的坐标为(4,0),点B的纵坐标是﹣1,则顶点A坐标是( )
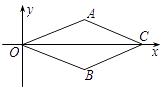
A.(2,1)
B.(1,﹣2)
C.(1,2)
D.(2,﹣1)
相关试题

