搜索
【题目】如图，在平面直角坐标系中，点P（1，﹣4）、Q（m，n）在函数
（x＞0）的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q分别作x轴、y轴的垂线，垂足为点C、D．QD交PA于点E，随着m的增大，四边形ACQE的面积（ ）
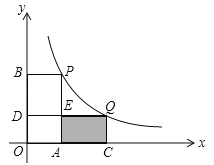
A．减小 B．增大 C．先减小后增大 D．先增大后减小
参考答案：
【答案】B．
【解析】
试题分析：AC=m﹣1，CQ=n，则S四边形ACQE=ACCQ=（m﹣1）n=mn﹣n．
∵Q（m，n）在函数
（x＞0）的图象上，∴mn=k=﹣4（常数），∴S四边形ACQE=ACCQ=（m﹣1）n=﹣4﹣n，∵当m＞1时，n随m的增大而减小，∴S四边形ACQE=﹣4﹣n随m的增大而增大．故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一元二次方程x2+3x=0的解是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知实数x满足(x2－x)2－4(x2－x)－5＝0，则x2－x的值是____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某建筑物AC顶部有一旗杆AB，且点A，B，C在同一条直线上，小明在地面D处观测旗杆顶端B的仰角为30°，然后他正对建筑物的方向前进了20米到达地面的E处，又测得旗杆顶端B的仰角为60°，已知建筑物的高度AC=12m，求旗杆AB的高度（结果精确到0.1米）．参考数据：
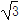≈1.73，
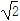≈1.41．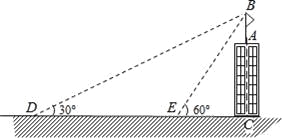
-
科目： 来源： 题型：
查看答案和解析>>【题目】感知：如图1，AD平分∠BAC．∠B+∠C=180°，∠B=90°，易知：DB=DC．
探究：如图2，AD平分∠BAC，∠ABD+∠ACD=180°，∠ABD＜90°，求证：DB=DC．
应用：如图3，四边形ABCD中，∠B=45°，∠C=135°，DB=DC=a，则AB﹣AC= （用含a的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】对角线互相的平行四边形是菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在菱形ABCD中，对角线AC与BD相交于点O，AB=8，∠BAD=60°，点E从点A出发，沿AB以每秒2个单位长度的速度向终点B运动，当点E不与点A重合时，过点E作EF⊥AD于点F，作EG∥AD交AC于点G，过点G作GH⊥AD交AD（或AD的延长线）于点H，得到矩形EFHG，设点E运动的时间为t秒
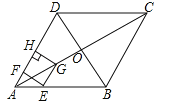
（1）求线段EF的长（用含t的代数式表示）；
（2）求点H与点D重合时t的值；
（3）设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位，求S与t之间的函数关系式；
（4）矩形EFHG的对角线EH与FG相交于点O′，当OO′∥AD时，t的值为 ；当OO′⊥AD时，t的值为 ．
相关试题
