搜索
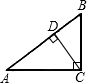
如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，BC=3，AC=4，设∠BCD=α，则tanα的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
参考答案：
分析：证明∠BCD=∠A=α，在Rt△ABC中求tanα的值．
解答：解：∵∠ACB=90°，CD⊥AB，
∴∠BCD+∠B=90°，∠A+∠B=90°，
∴∠BCD=∠A=α．
∴tanα=tanA=
=
．
故选A．
∴∠BCD+∠B=90°，∠A+∠B=90°，
∴∠BCD=∠A=α．
∴tanα=tanA=
| BC |
| AC |
| 3 |
| 4 |
故选A．
点评：考查灵活进行等量转换的能力．
-
科目： 来源： 题型：
查看答案和解析>>23、如图，Rt△ABC中，∠ACB=90°，∠CAB=30°，用圆规和直尺作图，用两种方法把它分成两个三角形，且要求其中一个三角形是等腰三角形．（保留作图痕迹，不要求写作法和证明）
-
科目： 来源： 题型：
查看答案和解析>>
如图，Rt△ABC中，∠ACB=90°，tanB=
，D是BC点边上一点，DE⊥AB于E，CD=DE，AC+CD=18．3 4
（1）求BC的长（2）求CE的长． -
科目： 来源： 题型：
查看答案和解析>>
如图，Rt△ABC中，∠C=90°，BC=3，AC=4，若△ABC∽△BDC，则CD=（ ） -
科目： 来源： 题型：
查看答案和解析>>
如图，Rt△ABC中，∠C=90°，△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F．
（1）若BC=40cm，AB=50cm，求⊙0的半径；
（2）若⊙0的半径为r，△ABC的周长为ι，求△ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>
如图，Rt△ABC中，∠ABC=90゜，BD⊥AC于D，∠CBD=α，AB=3，BC=4．
（1）求sinα的值；
（2）求AD的长．
相关试题
