【题目】如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A′E′F′.设P、P′分别是EF、E′F′的中点,当点A′与点B重合时,四边形PP′F′F的面积为( )

A. 8![]() B. 4
B. 4![]() C. 12
C. 12![]() D. 8
D. 8![]() -8
-8
参考答案:
【答案】B
【解析】
过点P作PM⊥AF于点M,首先证明四边形PP′F′F是平行四边形,求出PM即可解决问题.
解:过点P作PM⊥AF于点M,

由题意PF=P′F′,PF∥P′F′ ,
∴四边形PP′F′F是平行四边形,
∵四边形ABCD是菱形,∠A=60°,
由平移性质可得AF=BF′,所以FF′=AB=8,
∵∠A=60°,AD=8,F是AB的中点,AB=8,FE⊥AD,
∴AF=![]() AB=4,∠AFE=30°,AE=
AB=4,∠AFE=30°,AE=![]() AF=2,由勾股定理得:EF=2
AF=2,由勾股定理得:EF=2![]()
∵P是EF的中点,∴PF=![]() EF=
EF= ![]() ,
,
又∵∠PFM=30°,∴PM=![]() PF=
PF=![]() ,
,
∴S平行四边形PP′F′F= F′F×PM=8×![]() =4
=4![]() .
.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=x2+bx+c的图象过点A(1,0)和C(0,﹣3)
(1)求这个二次函数的解析式;
(2)如果这个二次函数的图象与x轴的另一个交点为B,求线段AB的长.
(3)在这条抛物线上是否存在一点P,使△ABP的面积为8?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )

A. AB∥CD,AD∥BC B. OA=OC,OB=OD C. AD=BC,AB∥CD D. AB=CD,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程组 :

(2)解不等式

(3)利用简单方法计算:

(4)因式分解:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点顺时针方向旋转180°后得到四边形A1B1C1D1 .

(1)写出点D1的坐标________;
(2)将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若点D2(4,5),画出平移后的图形;
(3)求点D旋转到点D1所经过的路线长.
-
科目: 来源: 题型:
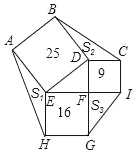
查看答案和解析>>【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
相关试题

