【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,边
,边![]() 上有一点
上有一点![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,联结
上,联结![]() ,
,![]() ,联结
,联结![]() ,
,![]() ,
,![]() .
.
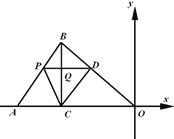
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在射线
在射线![]() 上,
上,![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)直线AB解析式为y=![]() x+9,P点坐标为(-
x+9,P点坐标为(-![]() ,2)(2)C点坐标为(-2,0)(3)R(2,-6).
,2)(2)C点坐标为(-2,0)(3)R(2,-6).
【解析】
(1)由A、B两点的坐标,利用待定系数法可求得直线AB的解析式,再把P点坐标代入直线解析式可求得P点坐标;
(2)由条件可证明△BPQ≌△CDQ,可证得四边形BDCP为平行四边形,由B、P的坐标可求得BP的长,则可求得CD的长,利用平行线分线段成比例可求得OC的长,则可求得C的坐标;
(3)由条件可知AR∥BO,故可先求出直线OB,BC的解析式,再根据直线平行求出AR的解析式,联立直线AR、BC即可求出R点坐标.
(1)设直线AB解析式为y=kx+b,
把A、B两点坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线AB解析式为y=![]() x+9,
x+9,
∵![]() 在直线AB上,
在直线AB上,
∴2=![]() m+9,解得m=-
m+9,解得m=-![]() ,
,
∴P点坐标为(-![]() ,2);
,2);
(2)∵![]() ,
,
∴∠PBQ=∠DCQ,
在△PBQ和△DCQ中
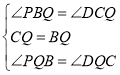

∴△PBQ≌△DCQ(ASA),
∴BP=CD,
∴四边形BDCP为平行四边形,
∵![]() ,(-
,(-![]() ,2),
,2),
∴CD=BP=![]() ,
,
∵A(-6,0),
∴OA=6,AB=![]() ,
,
∵CD∥AB,
∴△COD∽△AOB
∴![]() ,即
,即 ,解得CO=2,
,解得CO=2,
∴C点坐标为(-2,0);
(3)∵![]() ,
,
∴点A和点R到BO的距离相等,
∴BO∥AR,
设直线BO的解析式为y=nx,把![]() 代入得3=-4n,解得n=-
代入得3=-4n,解得n=-![]() x
x
∴直线BO的解析式为y=-![]() x,
x,
∴设直线AR的解析式为y=-![]() x+e,
x+e,
把A(-6,0)代入得0=-![]() ×(-6)+e
×(-6)+e
解得e=-![]()
∴直线AR的解析式为y=-![]() x-
x-![]() ,
,
设直线BC解析式为y=px+q,
把C、B两点坐标代入可得![]() ,解得
,解得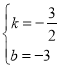 ,
,
∴直线AB解析式为y=-![]() x-3,
x-3,
联立
解得![]()
∴R(2,-6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:
①abc>0;②b2=4ac; ③4a+2b+c>0;④3a+c>0,

其中,正确的结论是______.(写出正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人)
…
200
250
300
350
400
…
y(元)
…
-20
-10
0
10
20
…
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A. 对我市市民实施低碳生活情况的调查
B. 对我国首架大型民用飞机零部件的检查
C. 对全国中学生心理健康现状的调查
D. 对市场上的冰淇淋质量的调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是我国东汉初年编订的一部数学经典著作在它的“方程”一章里,一次方程组是由算筹布置而成的《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2图中各行从左到右列出的算筹数分别表示未知数
 的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是
的系数与相应的常数项把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 类似地,图2所示的算筹图我们可以表述为( )
类似地,图2所示的算筹图我们可以表述为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】假设某商场地下停车场有5个出入口,每天早晨7点开始对外停车且此时车位空置率为80%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满2019年元旦节期间,由于商场人数增多,早晨7点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨7点开始经过_____小时车库恰好停满.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在菱形
 中,
中, ,
,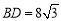 ,点
,点 是
是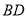 上一点,点
上一点,点 在
在 上,且
上,且 ,设
,设 .
.
(1)当
 时,如图2,求
时,如图2,求 的长;
的长;
(2)设
 ,求
,求 关于
关于 的函数关系式及其定义域;
的函数关系式及其定义域;(3)若
 是以
是以 为腰的等腰三角形,求
为腰的等腰三角形,求 的长.
的长.
相关试题

