【题目】如下图所示,直线y=-![]() x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标;
(2)若△OQC是等腰直角三角形,则t的值为________;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数表达式.

参考答案:
【答案】(1)点C的坐标为(2,2);(2)t的值为2或4;(3)直线CQ对应的函数表达式为y=-2x+6.
【解析】
(1)以![]() 和
和![]() 组成二元一次方程组,解此方程组即可求得点C的坐标;
组成二元一次方程组,解此方程组即可求得点C的坐标;
(2)由题意可知,∠COQ是锐角,由此可得若△COQ是等腰直角三角形,存在以下两种情况:①∠CQO=90°;②∠OCQ=90°;根据两种情况画出图形,结合已知条件分析解答即可求得对应的t的值;
(3)由题意可知,当点Q是线段OA的中点时,CQ平分△OCA的面积,由此结合已知条件求得点线段OA的中点的坐标即可求得此时CQ的解析式了.
(1)由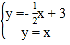 解得:
解得:![]() ,
,
∴点C的坐标为(2,2).
(2) 由题意可知,∠COQ是锐角,由此可得若△COQ是等腰直角三角形,存在以下两种情况:①∠CQO=90°;②∠OCQ=90°;先分别解答如下:
I、如图①,当∠CQO=90°,CQ=OQ时,
∵C(2,2),
∴OQ=CQ=2,解得:t=2;

II、如图②,当∠OCQ=90°,OC=CQ时,过点C作CM⊥OA于点M,
∵C(2,2),
∴CM=OM=2,
∴QM=OM=2,
∴OQ=4,
∴t=4.
综上所述,若△OCQ是等腰直角三角形,则t的值为2或4.
(3)令-![]() x+3=0,得x=6,
x+3=0,得x=6,
∴A(6,0).
∴点Q的坐标为(3,0)时,CQ平分△OCA的面积.
设直线CQ的函数表达式为y=kx+b.
把C(2,2),Q(3,0)代入y=kx+b得:
![]() ,
,
解得k=-2,b=6,
∴当直线CQ平分△OCA的面积时,其对应的函数表达式为y=-2x+6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:y=﹣
 x与反比例函数y=
x与反比例函数y= 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:(1)求反比例函数的表达式;
(2)将直线l1:y=﹣
 x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y= 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为半圆直径,
为半圆直径, 、
、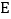 为圆周上两点,且
为圆周上两点,且 ,
, 与
与 交于点
交于点 ,则图中与
,则图中与 相等的角有( )
相等的角有( )
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D. 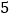 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等腰直角
是等腰直角 外一点,把
外一点,把 绕直角顶点
绕直角顶点 顺时针旋转
顺时针旋转 到
到 ,已知
,已知 ,
, ,则
,则 的值为________.
的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
, ,
, .
. 如图①,将线段
如图①,将线段 绕点
绕点 顺时针旋转
顺时针旋转 ,所得到与
,所得到与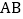 交于点
交于点 ,则
,则 的长
的长 ________;
________; 如图②,点
如图②,点 是边
是边 上一点
上一点 且
且 ,将线段
,将线段 绕点
绕点 旋转,得线段
旋转,得线段 ,点
,点 始终为
始终为 的中点,则将线段
的中点,则将线段 绕点
绕点 逆时针旋转________度时,线段
逆时针旋转________度时,线段 的长最大,最大值为________.
的长最大,最大值为________.
-
科目: 来源: 题型:
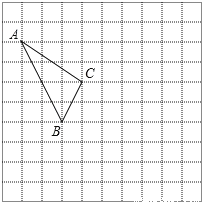
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)写出点B的坐标;
(3)将△ABC向右平移5个单位长度,向下平移2个单位长度,画出平移后的图形△A′B′C′;
(4)计算△A′B′C′的面积﹒
(5)在x轴上存在一点P,使PA+PC最小,直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, 是圆
是圆 的两条直径,连接
的两条直径,连接 ,
, .
. 如图①,求证:
如图①,求证: ,
, ;
; 如图②,过点
如图②,过点 作
作 于点
于点 ,交圆
,交圆 于点
于点 ,在
,在 上取一点
上取一点 ,使
,使 ,
,求证:四边形
 是平行四边形.
是平行四边形.
相关试题

