【题目】如图,![]() 是等腰直角
是等腰直角![]() 外一点,把
外一点,把![]() 绕直角顶点
绕直角顶点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,已知
,已知![]() ,
,![]() ,则
,则![]() 的值为________.
的值为________.

参考答案:
【答案】1:2
【解析】
如图,连接AP,构建全等三角形:△ABP≌△CBP′(SAS),由该全等三角形的对应边相等得到AP=P′C;如图,连接PP′,结合已知条件可以推知△APP′是直角三角形,所以由勾股定理来求相关线段的长度即可.
如图,连接AP,

∵BP绕点B顺时针旋转![]() 到BP′,
到BP′,
∴BP=BP′,∠ABP+∠ABP′=![]() ,
,
又∵△ABC是等腰直角三角形,
∴AB=BC,∠CBP′+∠ABP′=![]() ,
,
∴∠ABP=∠CBP′,
在△ABP和△CBP′中,
∵
∴△ABP≌△CBP′(SAS),
∴AP=P′C,
∵P′A:P′C=1:3,
∴AP=3P′A,
连接PP′,则△PBP′是等腰直角三角形,
∴![]()
∵![]()
∴![]()
∴△APP′是直角三角形,
设P′A=x,则AP=3x,
根据勾股定理,![]()
∴![]()
解得PB=2x,
∴P′A:PB=x:2x=1:2.
故答案为:1:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1:y=﹣
 x与反比例函数y=
x与反比例函数y= 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:(1)求反比例函数的表达式;
(2)将直线l1:y=﹣
 x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y= 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为半圆直径,
为半圆直径, 、
、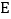 为圆周上两点,且
为圆周上两点,且 ,
, 与
与 交于点
交于点 ,则图中与
,则图中与 相等的角有( )
相等的角有( )
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D. 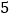 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示,直线y=-
 x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.(1)求出点C的坐标;
(2)若△OQC是等腰直角三角形,则t的值为________;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,
, ,
, .
. 如图①,将线段
如图①,将线段 绕点
绕点 顺时针旋转
顺时针旋转 ,所得到与
,所得到与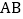 交于点
交于点 ,则
,则 的长
的长 ________;
________; 如图②,点
如图②,点 是边
是边 上一点
上一点 且
且 ,将线段
,将线段 绕点
绕点 旋转,得线段
旋转,得线段 ,点
,点 始终为
始终为 的中点,则将线段
的中点,则将线段 绕点
绕点 逆时针旋转________度时,线段
逆时针旋转________度时,线段 的长最大,最大值为________.
的长最大,最大值为________.
-
科目: 来源: 题型:
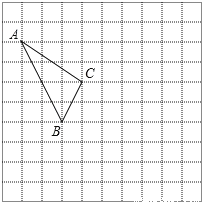
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)写出点B的坐标;
(3)将△ABC向右平移5个单位长度,向下平移2个单位长度,画出平移后的图形△A′B′C′;
(4)计算△A′B′C′的面积﹒
(5)在x轴上存在一点P,使PA+PC最小,直接写出点P的坐标.
相关试题

