【题目】如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( ) 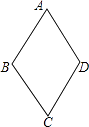
A.52cm
B.40cm
C.39cm
D.26cm
参考答案:
【答案】A
【解析】解: 如图,连接AC、BD相交于点O,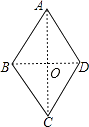
∵四边形ABCD的四边相等,
∴四边形ABCD为菱形,
∴AC⊥BD,S四边形ABCD= ![]() ACBD,
ACBD,
∴ ![]() ×24BD=120,解得BD=10cm,
×24BD=120,解得BD=10cm,
∴OA=12cm,OB=5cm,
在Rt△AOB中,由勾股定理可得AB= ![]() =13(cm),
=13(cm),
∴四边形ABCD的周长=4×13=52(cm),
故选A.
可定四边形ABCD为菱形,连接AC、BD相交于点O,则可求得BD的长,在Rt△AOB中,利用勾股定理可求得AB的长,从而可求得四边形ABCD的周长.
-
科目: 来源: 题型:
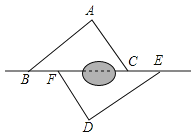
查看答案和解析>>【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+b2+2a-4b+5=0,求2a2+4b-3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)4(x﹣1)=1﹣x
(2)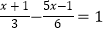 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图),图中从左到右依次为第1,2,3,4,5组.
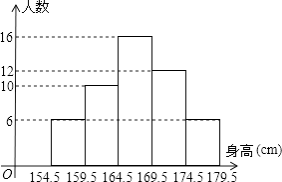
(1)求抽取了多少名男生测量身高?
(2)身高在哪个范围内的男生人数最多?(答出是第几小组即可)
(3)若该中学有300名男生,请估计身高为170cm及170cm以上的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
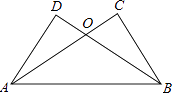
求证:
(1)BC=AD
(2)△OAB是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=( )
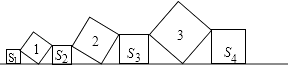
A.5
B.4
C.6
D.10
相关试题

