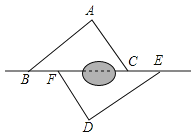
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)AB∥DE,AC∥DF.
【解析】
试题分析:(1)先证明BC=EF,再根据SSS即可证明.
(2)结论AB∥DE,AC∥DF,根据全等三角形的性质即可证明.
试题解析:(1)证明:∵BF=CE,∴BF+FC=FC+CE,即BC=EF,在△ABC和△DEF中,∵AB=DE,AC=DF,BC=EF,∴△ABC≌△DEF(SSS).
(2)结论:AB∥DE,AC∥DF.
理由:∵△ABC≌△DEF,∴∠ABC=∠DEF,∠ACB=∠DFE,∴AB∥DE,AC∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程3x(x﹣1)=5(x+2)化为一元二次方程的一般式,正确的是( )
A.4x2﹣4x+5=0B.3x2﹣8x﹣10=0C.4x2+4x﹣5=0D.3x2+8x+10=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:

(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
-
科目: 来源: 题型:
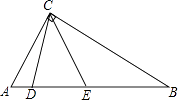
查看答案和解析>>【题目】如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,则∠DCE的大小为(度).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+b2+2a-4b+5=0,求2a2+4b-3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)4(x﹣1)=1﹣x
(2)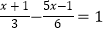 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( )
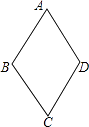
A.52cm
B.40cm
C.39cm
D.26cm
相关试题

