【题目】为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图),图中从左到右依次为第1,2,3,4,5组.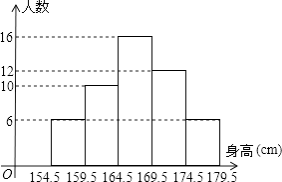
(1)求抽取了多少名男生测量身高?
(2)身高在哪个范围内的男生人数最多?(答出是第几小组即可)
(3)若该中学有300名男生,请估计身高为170cm及170cm以上的人数.
参考答案:
【答案】
(1)解:6+10+16+12+6=50(名),
即抽取了50名男生测量身高
(2)解:身高在第3小组内的男生人数最多,为16人
(3)解:身高为170cm及170cm的频率= ![]() ,
,
∴身高为170cm及170cm以上的人数=300×0.36=108名
【解析】(1)根据频数分布直方图,求出各小组的数据之和即可。
(2)观察频数分布直方图可得出结果。
(3)观察频数分布直方图,身高为170cm及170cm以上的人数=该中学的男生人数![]() 身高为170cm及170cm的频率,计算即可。
身高为170cm及170cm的频率,计算即可。
【考点精析】解答此题的关键在于理解频数与频率的相关知识,掌握落在各个小组内的数据的个数为频数;每一小组的频数与数据总数(样本容量n)的比值叫做这一小组的频率,以及对频数分布直方图的理解,了解特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+b2+2a-4b+5=0,求2a2+4b-3的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)4(x﹣1)=1﹣x
(2)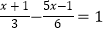 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的四边相等,且面积为120cm2 , 对角线AC=24cm,则四边形ABCD的周长为( )
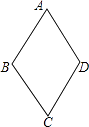
A.52cm
B.40cm
C.39cm
D.26cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
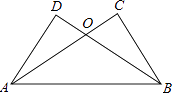
求证:
(1)BC=AD
(2)△OAB是等腰三角形. -
科目: 来源: 题型:
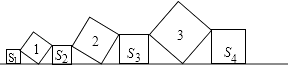
查看答案和解析>>【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=( )
A.5
B.4
C.6
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
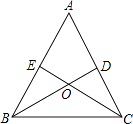
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
相关试题

