【题目】如图,AB是⊙O的直径,C,D为⊙O上两点,CF⊥AB于点F,CE⊥AD交AD的延长线于点E,且CE=CF. 
(1)求证:CE是⊙O的切线;
(2)连接CD,CB.若AD=CD=a,写出求四边形ABCD面积的思路. 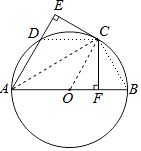
参考答案:
【答案】
(1)解:证明:连接OC,AC.
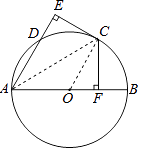
∵CF⊥AB,CE⊥AD,且CE=CF.
∴∠CAE=∠CAB.
∵OC=OA,
∴∠CAB=∠OCA.
∴∠CAE=∠OCA.
∴OC∥AE.
∴∠OCE+∠AEC=180°,
∵∠AEC=90°,
∴∠OCE=90°即OC⊥CE,
∵OC是⊙O的半径,点C为半径外端,
∴CE是⊙O的切线
(2)解:求解思路如下:
①由AD=CD=a,得到∠DAC=∠DCA,于是∠DCA=∠CAB,可知DC∥AB;
![]() =
= ![]() ,
,
②由OC∥AE,OC=OA,可知四边形AOCD是菱形;
③由∠CAE=∠CAB,得到CD=CB,DC=BC=a,可知△OBC为等边三角形;
④由等边△OBC可求高CF的长,进而可求四边形ABCD面积.
解:∵AD=CD,
∴∠DAC=∠DCA=∠CAB,
∴DC∥AB,
∵∠CAE=∠OCA,
∴OC∥AD,
∴四边形AOCD是平行四边形,
∴OC=AD=a,AB=2a,
∵∠CAE=∠CAB,
∴CD=CB=a,
∴CB=OC=OB,
∴△OCB是等边三角形,
在Rt△CFB中,CF= ![]() =
= ![]() ,
,
∴S四边形ABCD= ![]() (DC+AB)CF=
(DC+AB)CF= ![]() a2.
a2.
【解析】(1)连接OC,AC,可先证明AC平分∠BAE,结合圆的性质可证明OC∥AE,可得∠OCB=90°,可证得结论;(2)可先证得四边形AOCD为平行四边形,再证明△OCB为等边三角形,可求得CF、AB,利用梯形的面积公式可求得答案.
【考点精析】本题主要考查了角平分线的性质定理和垂径定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 平面内,没有公共点的两条线段平行
B. 平面内,没有公共点的两条射线平行
C. 没有公共点的两条直线互相平行
D. 互相平行的两条直线没有公共点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,BO 平分∠ABC,CO 平分∠ACB,MN 经过点 O,与 AB、AC 相交于点 M、N,且 MN∥BC,那么下列说法中:①∠MOB=∠MBO②△AMN 的周长等于 AB+AC;③∠A=2∠BOC﹣180°;④连接 AO,则
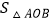 :
: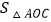 :
: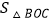 =AB:AC:BC;正确的有( )
=AB:AC:BC;正确的有( )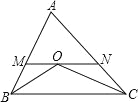
A. ①②④ B. ①②③ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角三角形 ABC 和锐角三角形 A'B'C'中,AD、A'D'分别是边 BC、B'C'上的高,且AB=A'B',AD=A'D'.要使△ABC≌△A'B'C',则应补充条件:________(填写一个即可)
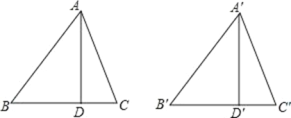
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点E在AC的延长线上,有下列条件∠1=∠2,②∠3=∠4,③∠A=∠DCE,④∠D=∠DCE,⑤∠A+∠ABD=180°,⑥∠A+∠ACD=180°,其中能判断AB∥CD的是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,AC=3,点I为Rt△ABC三条角平分线的交点,则点I到边AB的距离为_____.
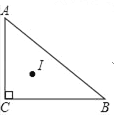
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CA⊥AB,垂足为 A,AB=24,AC=12,射线 BM⊥AB,垂足为 B, 一动点 E 从 A点出发以 3 厘米/秒沿射线 AN 运动,点 D 为射线 BM 上一动点, 随着 E 点运动而运动,且始终保持 ED=CB,当点 E 经过______秒时,△DEB 与△BCA 全等.

相关试题

