【题目】如图所示,点E在AC的延长线上,有下列条件∠1=∠2,②∠3=∠4,③∠A=∠DCE,④∠D=∠DCE,⑤∠A+∠ABD=180°,⑥∠A+∠ACD=180°,其中能判断AB∥CD的是_____.

参考答案:
【答案】①③⑥
【解析】
根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行可以进行判定.
①正确,根据内错角相等,两直线平行,若∠1=∠2,则AB∥CD,
②错误, 根据内错角相等,两直线平行,若∠3=∠4,则BD//AC,不能判定AB∥CD,
③正确, 根据同位角相等,两直线平行,若∠A=∠DCE,则AB∥CD,
④错误,根据内错角相等,两直线平行,若∠D=∠DCE则BD//AC,不能判定AB∥CD,
⑤错误, 根据同旁内角互补,两直线平行, 若∠A+∠ABD=180°, 则BD//AC,不能判定AB∥CD,
⑥正确,根据同旁内角互补,两直线平行, 若∠A+∠ACD=180°,则AB∥CD,
所以正确的有①③⑥,
故答案为: ①③⑥.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中以点A为圆心,AB为半径作圆A交网格于点C(如图(1)),过点C作圆的切线交网格于点D,以点A为圆心,AD为半径作圆交网格于点E(如图(2)). 问题:

(1)求∠ABC的度数;
(2)求证:△AEB≌△ADC;
(3)△AEB可以看作是由△ADC经过怎样的变换得到的?并判断△AED的形状(不用说明理由).
(4)如图(3),已知直线a,b,c,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形A′B′C′,使三个顶点A′,B′,C′,分别在直线a,b,c上.要求写出简要的画图过程,不需要说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A. 2,
 B. 4,3 C. 4,
B. 4,3 C. 4, D. 2,1
D. 2,1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2﹣2ax+c(a<0)的图象与x轴负半轴交于点A(﹣1,0),与y轴正半轴交于点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过A、B.

(1)求一次函数解析式;
(2)求顶点P的坐标;
(3)平移直线AB使其过点P,如果点M在平移后的直线上,且 ,求点M坐标;
,求点M坐标;
(4)设抛物线的对称轴交x轴于点E,连接AP交y轴于点D,若点Q、N分别为两线段PE、PD上的动点,连接QD、QN,请直接写出QD+QN的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面题目的计算过程:
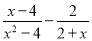
=
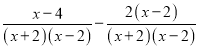 ①
①=x﹣4﹣2(x﹣2)②
=x﹣4﹣2x+4③
=﹣x④
(1)上述计算过程中,从哪一步开始出现错误?请写出错误步骤的序号 ;
(2)错误原因是 ;
(3)写出本题的正确解法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读图1的情景对话,然后解答问题:

(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是命题(填“真”或“假”)
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图2,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆 的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE. ①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,小红将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得AB=15,AD=12.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
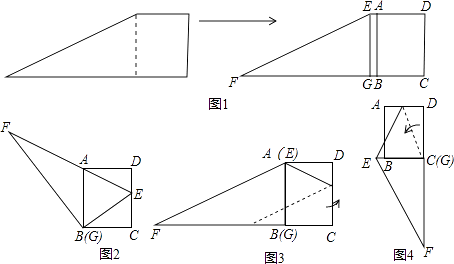
(1)将△EFG的顶点G移到矩形的顶点B处,再将三角形绕点B顺时针旋转使E点落在CD边上,此时,EF恰好经过点A(如图2)求FB的长度;
(2)在(1)的条件下,小红想用△EFG包裹矩形ABCD,她想了两种包裹的方法如图3、图4,请问哪种包裹纸片的方法使得未包裹住的面积大?(纸片厚度忽略不计)请你通过计算说服小红.
相关试题

