【题目】如图,一次函数![]() 的图像分别与
的图像分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,以线段
,以线段![]() 为边在第一象限内作等腰直角三角形
为边在第一象限内作等腰直角三角形![]() ,
,![]() ,则过
,则过![]() 、
、![]() 两点的直线对应的函数表达式为________.
两点的直线对应的函数表达式为________.

参考答案:
【答案】![]()
【解析】
作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,AD=OB,故可得出C点坐标,再用待定系数法即可求出直线BC的解析式.
解:如图所示:作CD⊥x轴于点D.
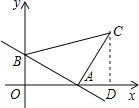
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
在△ABO与△CAD中,
 ,
,
∴△ABO≌△CAD(AAS),
∴AD=OB=2,CD=OA=3,
∴OD=OA+AD=5.
则点C的坐标是(5,3).
设直线BC的解析式是y=kx+b,
根据题意得:![]() ,
,
解得: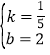 ,
,
则直线BC的解析式是:y=![]() x+2.
x+2.
故答案为::y=![]() x+2.
x+2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
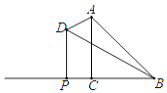
A.一直变大
B.一直变小
C.先变小再变大
D.先变大再变小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(0,2)、B(
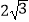 ,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则:
,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则: 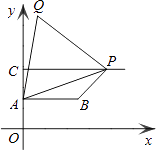
(1)当AB为梯形的底时,点P的横坐标是;
(2)当AB为梯形的腰时,点P的横坐标是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】学习成为商城人的时尚,义乌市新图书馆的启用,吸引了大批读者.有关部门统计了2011年10月至2012年3月期间到市图书馆的读者的职业分布情况,统计图如下:
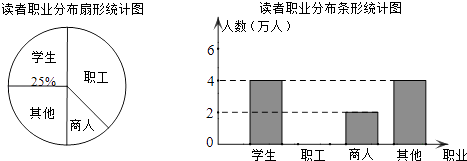
(1)在统计的这段时间内,共有万人到市图书馆阅读,其中商人所占百分比是 ,
(2)将条形统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);
(3)若今年4月到市图书馆的读者共28000名,估计其中约有多少名职工? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.

(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在烧开水时,水温达到100℃就会沸腾,下表是某同学做“观察水的沸腾”实验时记录的数据:

(1)上表反映了哪两个量之间的关系?哪个是自变量?哪个是因变量?
(2)水的温度是如何随着时间的变化而变化的?
(3)时间推移2分钟,水的温度如何变化?
(4)时间为8分钟时,水的温度为多少?你能得出时间为9分钟时,水的温度吗?
(5)根据表格,你认为时间为16分钟和18分钟时水的温度分别为多少?
(6)为了节约能源,你认为应在什么时间停止烧水?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数
 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=  .
.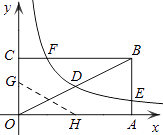
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
相关试题

