【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(Ⅰ)请写出AF与BE的数量关系与位置关系分别是什么,并证明.
(Ⅱ)如图2,若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF,且EA=ED=FD=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
参考答案:
【答案】试题
【解析】(Ⅰ)AF=BE,AF⊥BE. 证明参考(Ⅱ)
(Ⅱ)结论成立. 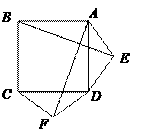
证明:∵四边形ABCD是正方形,
∴BA=AD =DC,∠BAD =∠ADC = 90°.
在△EAD和△FDC中, 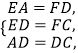
∴△EAD≌△FDC.
∴∠EAD=∠FDC.
∴∠EAD+∠DAB=∠FDC+∠CDA,即∠BAE=∠ADF.
在△BAE和△ADF中, 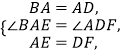
∴△BAE≌△ADF.
∴BE = AF,∠ABE=∠DAF.
∵∠DAF +∠BAF=90°,
∴∠ABE +∠BAF=90°,
∴AF⊥BE.
(Ⅰ)根据SAS易证△ADE≌△DCF,即可证明AF与BE的数量关系是AF=BE,位置关系是AF⊥BE; (Ⅱ)成立,证明△ADE≌△DCF,然后证明△ABE≌△ADF即可证得BE=AF,然后根据三角形内角和定理证明∠AMB=90°,从而结论得证.
【考点精析】关于本题考查的三角形的内角和外角,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于0的说法中错误的是( )
A.0是绝对值最小的数
B.0的相反数是0
C.0是整数
D.0的倒数是0 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)
(2)(﹣a3)2﹣a2a4+(2a4)2÷a2
(3)(2a﹣3b)2﹣4a(a﹣3b)
(4)(3﹣2x)(3+2x)+4 (2﹣x)2(本题先化简,再求值,其中x=﹣0.25) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,一只蚂蚁从点P(0,1)出发,沿着图示折线方向移动,第一次到达点(1,1),第二次达到点(1,0),第三次达到点(1,﹣1),第四次达到点(2,﹣1),…,按照这样的规律,第2016次到达点的坐标应为 .
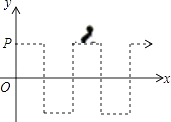
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. 5a-3a=2 B. 3x2+2x=5x3 C. -8ab+5ab=-3ab D. 2x2y-2xy2=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( ).
A. 一个游戏的中奖概率是
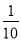 ,则做10次这样的游戏一定会中奖
,则做10次这样的游戏一定会中奖B. 一组数据6,8,7,8,8,9,10的众数和中位数都是8
C. 为了解全国中学生的心理健康情况,应该采用普查的方式
D. 若甲组数据的方差S2甲=0.01,乙组数据的方差S2乙=0.1,则乙组数据比甲组数据稳定
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成证明,说明理由. 已知:如图,点D在BC边上,DE、AB交于点F,AC∥DE,∠1=∠2,∠3=∠4.
求证:AE∥BC.
证明:∵AC∥DE(已知),
∴∠4=()
∵∠3=∠4(已知),
∴∠3=()
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD()
即∠FAC=∠EAD,
∴∠3= .
∴AE∥BC()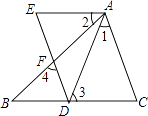
相关试题

