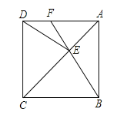
【题目】如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
(1)求证:△BCE≌△DCE;
(2)延长BE交AD于点F,若∠DEB=140,求∠AFE的度数.
参考答案:
【答案】(1)、证明过程见解析;(2)、65°.
【解析】
试题分析:(1)、根据正方形的性质可得BC=DC,∠BCE=∠CDE=45°,根据CE=CE得出三角形全等;(2)、根据全等得出∠BEC=∠DEC=70°,根据△BCE的内角和得出∠CBE=65°,根据平行线的性质得出∠AFE=∠CBE.
试题解析:(1)、∵正方形ABCD中,E为对角线AC上一点,
∴BC=DC,∠BCE=∠DCE=45 又∵CE=CE ∴△BCE≌△DCE(SAS)
(2)、由全等可知,∠BEC=∠DEC=![]() ∠DEB=
∠DEB=![]() ×140=70
×140=70
在△BCE中,∠CBE=180―70―45=65
∴在正方形ABCD中,AD∥BC,有∠AFE=∠CBE=65
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+bx+c=0的两根为x1=1,x2=2,则x2+bx+c分解因式的结果为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大连市内与庄河两地之间的距离是160千米,若汽车以平均每小时80千米的速度从大连市内开往庄河,则汽车距庄河的路程y(千米)与行驶的时间x(小时)之间的函数关系式为_____.
-
科目: 来源: 题型:
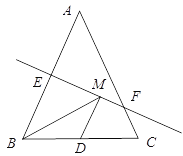
查看答案和解析>>【题目】如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为______cm.
-
科目: 来源: 题型:
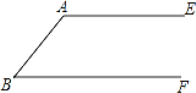
查看答案和解析>>【题目】如图,AE∥BF,先按(1)的要求作图,再按(2)的要求证明
(1)用直尺和圆规作出∠ABF的平分线BD交AE于点D,再作出BD的中点O(不写作法,保留作图痕迹)
(2)连接(1)所作图中的AO并延长与BF相交于点C,连接DC,求证:四边形ABCD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为6的正六边形外接圆半径是_____.
相关试题

