【题目】某批发商计划将一批海产品由A地运往B地.汽车货运公司和铁路货运公司均开办海产品运输业务.已知运输路程为120千米,汽车和火车的速度分别为60千米/时、100千米/时.两货运公司的收费项目及收费标准如下表所示:
运输工具 | 运输费单价/ (元/吨·千米) | 冷藏费单价/ (元/吨·小时) | 过路费/元 | 装卸及管理费/元 |
汽 车 | 2 | 5 | 200 | 0 |
火 车 | 1.8 | 5 | 0 | 1600 |
注:“元/吨·千米”表示每吨货物每千米的运费;“元/吨·小时”表示每吨货物每小时的冷藏费.
(1)设该批发商待运的海产品有x(吨),汽车货运公司和铁路货运公司所要收取的费用分别为y1(元)和y2(元),试求y1、y2与x之间的函数关系式.
(2)若该批发商待运的海产品不少于30吨,为节省运费,他应选择哪个货运公司承担运输业务?
参考答案:
【答案】(1)y1=250x+200、y2=222x+1 600 ;(2)50吨以下选汽车,50吨以上选火车,50吨时费用相同
【解析】试题分析:
(1)根据表格中提供的数据按题中所给数量关系列出两个函数关系式即可;
(2)根据(1)中所得函数解析式,分别由![]() 列出对应的不等式和方程,解不等式和方程即可求得本题答案.
列出对应的不等式和方程,解不等式和方程即可求得本题答案.
试题解析:
(1)由题意可得: ![]() ,即
,即![]() ;
;
![]() ,即
,即![]() ;
;
(2)由![]() 得:
得: ![]() ,解得:
,解得: ![]() ;
;
由![]() 可得:
可得: ![]() ,解得:
,解得: ![]() ;
;
由![]() 可得:
可得: ![]() ,解得:
,解得: ![]() ;
;
即:当运送量少于50吨时,选汽车运输;当运送量为50吨时,两种运输方式花费一样多;的运送量多于50吨时,选火车运输更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b 的图象与反比例函数y=
 的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:
的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:(1)一次函数的解析式;
(2)△AOB的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=y1+y2,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=﹣5;当x=2时,y=﹣7.
(1)求y与x的函数关系式;
(2)当y=5时,求x的值.
-
科目: 来源: 题型:
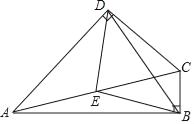
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点.(1)求证:△BED是等腰三角形:
(2)当∠BCD=_____°时,△BED是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

-
科目: 来源: 题型:
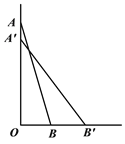
查看答案和解析>>【题目】如图,一架2.5米长的梯子斜立在竖直的墙上,此时梯足B距底端O为0.7米。(1)求OA的长度。(2)如果梯子顶端下滑0.4米,则梯子将滑出多少米?
相关试题

