【题目】已知y=y1+y2,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=﹣5;当x=2时,y=﹣7.
(1)求y与x的函数关系式;
(2)当y=5时,求x的值.
参考答案:
【答案】(1)![]() ;(2)y=5时,x=﹣2或x=﹣
;(2)y=5时,x=﹣2或x=﹣![]() .
.
【解析】(1)根据题意,可设y1=k1(x+1),![]() ;代入数据可得答案;
;代入数据可得答案;
(2)将y=5代入由(1)可得解析式中,解可得答案.
试题解析:解:(1)设y1=k1(x+1),![]() ;
;
则有: ![]() .
.
∵当x=0时,y=﹣5;当x=2时,y=﹣7,∴有 .
.
解得:k1=﹣2,k2=﹣3.
y与x的函数关系式为: ![]() ;
;
(2)把y=5代入![]() 可得:
可得: ![]() ,去分母得:﹣2(x+1)2﹣3=5(x+1),整理得:2x2+9x+10=0,即(x+2)(2x+5)=0,解得:x=﹣2或x=﹣
,去分母得:﹣2(x+1)2﹣3=5(x+1),整理得:2x2+9x+10=0,即(x+2)(2x+5)=0,解得:x=﹣2或x=﹣![]() .
.
经检验:x=﹣2或x=﹣![]() 是原方程的解,则y=5时,x=﹣2或x=﹣
是原方程的解,则y=5时,x=﹣2或x=﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数
 的图象交于点B、E.
的图象交于点B、E.(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标;
(3)连结
 、
、 、
、 ,求△
,求△ 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/时;④乙先到达B地.其中正确的是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b 的图象与反比例函数y=
 的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:
的图交象于A、B两点,且点A的横坐标和点B的纵坐标都是-2 , 求:(1)一次函数的解析式;
(2)△AOB的面积
-
科目: 来源: 题型:
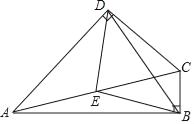
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点.(1)求证:△BED是等腰三角形:
(2)当∠BCD=_____°时,△BED是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某批发商计划将一批海产品由A地运往B地.汽车货运公司和铁路货运公司均开办海产品运输业务.已知运输路程为120千米,汽车和火车的速度分别为60千米/时、100千米/时.两货运公司的收费项目及收费标准如下表所示:
运输工具
运输费单价/
(元/吨·千米)
冷藏费单价/
(元/吨·小时)
过路费/元
装卸及管理费/元
汽 车
2
5
200
0
火 车
1.8
5
0
1600
注:“元/吨·千米”表示每吨货物每千米的运费;“元/吨·小时”表示每吨货物每小时的冷藏费.
(1)设该批发商待运的海产品有x(吨),汽车货运公司和铁路货运公司所要收取的费用分别为y1(元)和y2(元),试求y1、y2与x之间的函数关系式.
(2)若该批发商待运的海产品不少于30吨,为节省运费,他应选择哪个货运公司承担运输业务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

相关试题

