【题目】如图,长方形ABCD中,AB=4,AD=2,点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P、Q两点相遇时,它们同时停止运动。设Q点运动的时间为![]() (秒),在整个运动过程中,求解下面问题:
(秒),在整个运动过程中,求解下面问题:
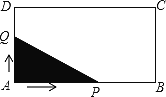
(1)当P、Q相遇时,求出![]() 的值(列方程解决问题);
的值(列方程解决问题);
(2)当△APQ的面积为![]() 时,此时t的值是_________;
时,此时t的值是_________;
(3)当△APQ为直角三角形时,直接写出相应的![]() 的值或取值范围.
的值或取值范围.
参考答案:
【答案】(1 t=3;(2)1或![]() ;(3)t=2或0<t≤
;(3)t=2或0<t≤![]() .
.
【解析】
(1)设t秒后相遇,根据相遇时共走了12个单位的路程列方程求解;
(2)分两种情形分别构建方程即可解决问题;
(3)由题意可得当0<x≤![]() ,△AQM是直角三角形,当
,△AQM是直角三角形,当 ![]() <x<2时△AQM是锐角三角形,当x=2时,△AQM是直角三角形,当2<x<3时△AQM是钝角三角形.
<x<2时△AQM是锐角三角形,当x=2时,△AQM是直角三角形,当2<x<3时△AQM是钝角三角形.
解:(1)设t秒后相遇,由题意得
t+3t=12,
∴t=3.
(2)由题意:当P、Q分别在AD、AB上时,
![]() t3t=
t3t=![]() ,解得t=或-1(舍弃),
,解得t=或-1(舍弃),
当P、Q都在CD上时,
![]() ×(12-4t)×2=
×(12-4t)×2=![]() ,解得t=
,解得t=![]() ,
,
综上所述,t=1或![]() 时,△APQ的面积为
时,△APQ的面积为![]() .
.
(3)当点P在AB上时,点Q在AD上时,此时△APQ为直角三角形,则0<x≤![]() ;
;
当点P在BC上时,点Q在AD上时,此时△APQ为锐角三角形,则![]() <x<2;
<x<2;
当点P在C处,此时点Q在D处,此时△APQ为直角三角形,则x=2时;
当点P在CD上时,点Q在DC上时,此时△APQ为钝角三角形,则2<x<3.
当△APQ为直角三角形时,相应的t的值或取值范围:0<x≤![]() 或x=2.
或x=2.
-
科目: 来源: 题型:
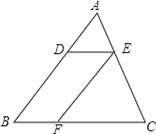
查看答案和解析>>【题目】如图,在△ABC中,DE∥BC,EF∥AB,若S△ADE=4cm2,S△EFC=9cm2,求S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某活动小组为了估计装有5个白球和若干个红球
 每个球除颜色外都相同
每个球除颜色外都相同 的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验
的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验 其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.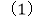 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少?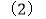 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复
 下表是活动进行中的一组统计数据:
下表是活动进行中的一组统计数据: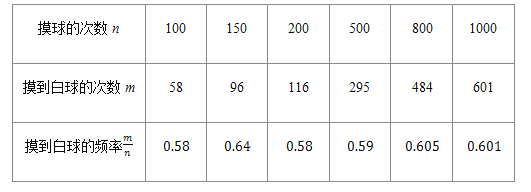
 请估计:当n很大时,摸到白球的频率将会接近______ ;
请估计:当n很大时,摸到白球的频率将会接近______ ; 精确到
精确到
 试估算口袋中白种颜色的球有多少只?
试估算口袋中白种颜色的球有多少只? 请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复
 下表是几次活动汇总后统计的数据:
下表是几次活动汇总后统计的数据: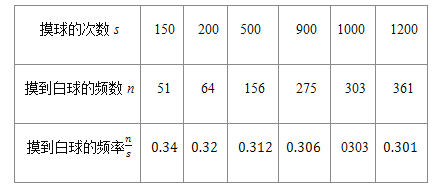
 请估计:当次数s很大时,摸到白球的频率将会接近______ ;假如你去摸一次,你摸到红球的概率是______
请估计:当次数s很大时,摸到白球的频率将会接近______ ;假如你去摸一次,你摸到红球的概率是______  精确到
精确到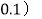 .
. 试估算口袋中红球有多少只?
试估算口袋中红球有多少只? 解决了上面的问题后请你从统计与概率方面谈一条启示.
解决了上面的问题后请你从统计与概率方面谈一条启示. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D为△ABC边BC的延长线上一点.∠ABC的角平分线与∠ACD的角平分线交于点M,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q,若∠A=48°,则∠BQC的度数为( )
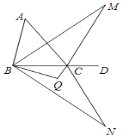
A. 138° B. 114° C. 102° D. 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过________小时车库恰好停满.
相关试题

