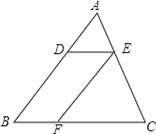
【题目】如图,在△ABC中,DE∥BC,EF∥AB,若S△ADE=4cm2,S△EFC=9cm2,求S△ABC.
参考答案:
【答案】25cm2.
【解析】试题分析:利用平行证明三角形相似,再利用相似的性质求三角形面积.
试题解析:
解:∵DE∥BC,EF∥AB,
∴∠A=∠FEC,∠AED=∠C,
∴△ADE∽△ECF;
∴S△ADE:S△ECF=(AE:EC)2,
∵S△ADE=4cm2,S△EFC=9cm2,
∴(AE:EC)2=4:9,
∴AE:EC=2:3,
即EC:AE=3:2,
∴(EC+AE):AE=5:2,
即AC:AE=5:2.
∵DE∥BC,
∴∠C=∠AED,
又∵∠A=∠A,
∴△ABC∽△ADE,
∴S△ABC:S△ADE=(AC:AE)2,
∴S△ABC:4=(5:2)2,
∴S△ABC=25cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 与
与 成正比例,且
成正比例,且 时,
时, .
.(1)求出
 与
与 之间的函数关系式;
之间的函数关系式;(2)在所给的直角坐标系(如图)中画出函数的图象;
(3)直接写出当
 时,自变量
时,自变量 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c是
 的三边,且满足
的三边,且满足 ,试判断
,试判断 的形状.
的形状.阅读下面解题过程:
解:由
 得:
得: ①
① ②
②即
 ③
③∴
 为Rt△.④
为Rt△.④试问:以上解题过程是否正确:_________.
若不正确,请指出错在哪步?______(填代号)
错误原因是______________________.
本题的结论应为_______________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线
 分别与x轴、y轴交于A、B两点,与直线
分别与x轴、y轴交于A、B两点,与直线 交于点
交于点 .平行于y轴的直线l从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;直线l分别交线段BC、OC、x轴于点D、E、P,以DE为斜边向左侧作等腰直角
.平行于y轴的直线l从原点O出发,以每秒1个单位长度的速度沿x轴向右平移,到C点时停止;直线l分别交线段BC、OC、x轴于点D、E、P,以DE为斜边向左侧作等腰直角 ,设直线l的运动时间为t(秒).
,设直线l的运动时间为t(秒).(1)填空:k=____;b=____;
(2)当t为何值时,点F在y轴上(如图2所示);
(3)设
 与
与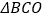 重叠部分的面积为S,请直接写出S与t的函数关系式(不要求写解答过程),并写出t的取值范围.
重叠部分的面积为S,请直接写出S与t的函数关系式(不要求写解答过程),并写出t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某活动小组为了估计装有5个白球和若干个红球
 每个球除颜色外都相同
每个球除颜色外都相同 的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验
的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共20组进行摸球实验 其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次.
其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做400次试验,汇总起来后,摸到红球次数为6000次. 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少? 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复
 下表是活动进行中的一组统计数据:
下表是活动进行中的一组统计数据: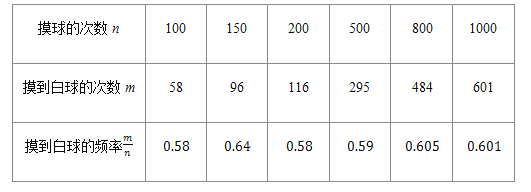
 请估计:当n很大时,摸到白球的频率将会接近______ ;
请估计:当n很大时,摸到白球的频率将会接近______ ; 精确到
精确到
 试估算口袋中白种颜色的球有多少只?
试估算口袋中白种颜色的球有多少只? 请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AB=4,AD=2,点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P、Q两点相遇时,它们同时停止运动。设Q点运动的时间为
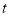 (秒),在整个运动过程中,求解下面问题:
(秒),在整个运动过程中,求解下面问题: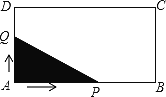
(1)当P、Q相遇时,求出
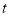 的值(列方程解决问题);
的值(列方程解决问题);(2)当△APQ的面积为
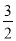 时,此时t的值是_________;
时,此时t的值是_________;(3)当△APQ为直角三角形时,直接写出相应的
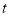 的值或取值范围.
的值或取值范围.
相关试题

