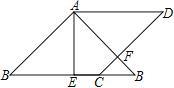
【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
A. 1 B. ![]() C. 2
C. 2![]() -2 D. 2-
-2 D. 2-![]()
参考答案:
【答案】D
【解析】由在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,可求得AE的长,由折叠易得△ABB′为等腰直角三角形,得到CB′=2BE-BC=2![]() -2,根据平行线的性质得到∠FCB′=∠B=45°,又由折叠的性质得到∠B′=∠B=45°,即可得到结论.
-2,根据平行线的性质得到∠FCB′=∠B=45°,又由折叠的性质得到∠B′=∠B=45°,即可得到结论.
∵在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,
∴AE=![]() ,由折叠易得△ABB′为等腰直角三角形,
,由折叠易得△ABB′为等腰直角三角形,
∴S△ABB′=![]() BAAB′=2,S△ABE=1,
BAAB′=2,S△ABE=1,
∴CB′=2BE-BC=2![]() -2,
-2,
∵AB∥CD,
∴∠FCB′=∠B=45°,
又由折叠的性质知,∠B′=∠B=45°,
∴CF=FB′=2-![]() .
.
故选D.
-
科目: 来源: 题型:
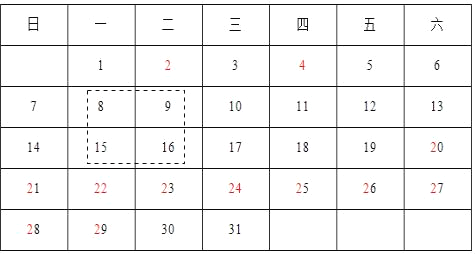
查看答案和解析>>【题目】如图所示为2013年7月份的日历示意图.
(1)请你计算虚线方框圈出的2×2个数(2行2列的4个数)的和;
(2)若方框圈出的2×2个数从左下角到右上角的2个数之和为46,则这4个数的最后一天是7月 日.(直接填空)
(3)若方框圈出的2×2个数的和最大,请你用方框将这4个数圈出来,并计算这4个数的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,绵阳市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
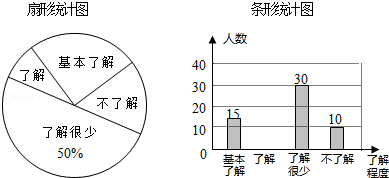
(1)接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;
(2)请补全条形统计图;
(3)若该中学共有学生3000人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=x+m的图象与反比例函数y2=
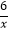 的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2 .
的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2 .
(1)求一次函数的函数表达式;
(2)已知反比例函数在第一象限的图象上有一点C到x轴的距离为2,求△ABC的面积.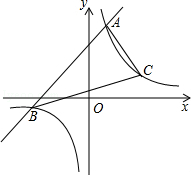
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、M、B、N、C在同一直线上顺次排列,点M是线段AB的中点,点N是线段MC的中点,点N在点B的右边.

(1)填空:图中共有线段 条;
(2)若AB=6,MC=7,求线段BN的长;
(3)若AB=a,MC=7,将线段BN的长用含a的代数式表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=24 cm,BC=26 cm.点P从A出发,以1 cm/s的速度向点D运动,点Q从点C同时出发,以3 cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.从运动开始,使PQ=CD需要__________秒
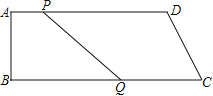
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=22.5°,E在AB上,且∠DCE=67.5°,DE⊥AB于E,若AE=1,线段BE的长为____________.

相关试题

