【题目】甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.

(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
参考答案:
【答案】(1)a=90,m=1.5,n=3.5。
(2)y与x的关系式为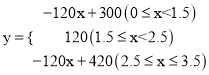
(3)乙车行驶了1小时或3小时
【解析】试题分析:(1)∵甲车途径C地时休息一小时,∴2.5﹣m=1。∴m=1.5。
∵乙车的速度为: ![]() ,即
,即![]() ,解得a=90。
,解得a=90。
甲车的速度为: ![]() ,解得n=3.5。
,解得n=3.5。
∴a=90,m=1.5,n=3.5。
(2)分休息前,休息时,休息后三个阶段,利用待定系数法求一次函数解析式解答。
(3)求出甲车的速度,然后分①相遇前两人的路程之和加上相距的120千米等于总路程列出方程求解即可;②相遇后,两人行驶的路程之和等于总路程加120千米,列出方程求解即可。
解:(1)a=90,m=1.5,n=3.5。
(2)设甲车的y与x的函数关系式为y=kx+b(k≠0),
①休息前,0≤x<1.5,函数图象经过点(0,300)和(1.5,120),
∴![]() ,解得
,解得![]() 。
。
∴y=﹣120x+300,
②休息时,1.5≤x<2.5,y=120。
③休息后,2.5≤x≤3.5,函数图象经过(2.5,120)和(3.5,0),
所以, ![]() ,解得
,解得![]() 。
。
∴y=﹣120x+420。
综上所述,y与x的关系式为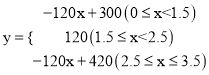 。
。
(3)设两车相距120千米时,乙车行驶了x小时,甲车的速度为:(300﹣120)÷1.5=120千米/时。
①若相遇前,则120x+60x=300﹣120,解得x=1。
②若相遇后,则120(x﹣1)+60x=300+120,解得x=3。
∴两车相距120千米时,乙车行驶了1小时或3小时。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于A(0,2),B(0,8),则圆心P的坐标是( )

A.(5,3)
B.(5,4)
C.(3,5)
D.(4,5) -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b(k≠0)的图象由直线y=3x向下平移得到,且过点A(1,2).
(1)求一次函数的解析式;
(2)求直线y=kx+b与x轴的交点B的坐标;
(3)设坐标原点为O,一条直线过点B,且与两条坐标轴围成的三角形的面积是
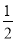 ,这条直线与y轴交于点C,求直线AC对应的一次函数的解析式.
,这条直线与y轴交于点C,求直线AC对应的一次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】若(a﹣2)x|a|﹣1﹣2=0是关于x的一元一次方程,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为cm.
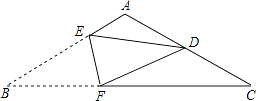
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是 时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是 时,它们一定不全等.
相关试题

