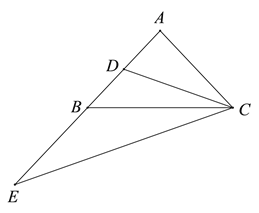
【题目】如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB至点E,使BE=AB,连接CE. 请你探究:
(1)当∠BAC为直角时,直接写出线段CE与CD之间的数量关系;
(2)当∠BAC为锐角或钝角时,(1)中的上述数量关系是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
参考答案:
【答案】(1)CE=2CD;(2)仍然成立
【解析】试题分析:(1)如图,延长CE到F,使EF=CE,连接FB.由CE是AB边上的中线,∠BEF=∠AEC,可证得△AEC≌△BEF,进而得∠1=∠A,FB=BD,从而可得△CDB≌△CFB,即可得到结果;
(2)根据上面的方法,直接可画图证明即可.
试题解析:(1)CE=2CD;
延长CE到F,使EF=CE,连接FB,
∵CE是AB边上的中线,
∴AE=BE,
又∵∠BEF=∠AEC,
∴△AEC≌△BEF,
∴FB=AC,∠1=∠A,
∵BD=AB,
∴FB=BD,
∵∠3=∠A+∠ACB=∠1+∠2,即∠CBD=∠CBF,
又∵BC为公共边,
∴△CDB≌△CFB,
∴CD=CF=2CE,
即2CE=CD
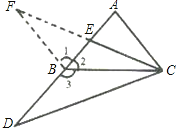
(2)仍然成立. 例如取AC中点M,连接BM. 证法较多,略。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)
 ;
;(2)
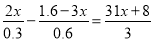 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为t.

(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】物体向右运动4m记作+4m,那么物体向左运动3m,应记作m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A. 形状相同的两个三角形是全等形
B. 面积相等的两个三角形全等
C. 周长相等的两个三角形全等
D. 周长相等的两个等边三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船以18海里/时的速度由西向东航行,在A处测得小岛C在北偏东75°方向上,两小时后,轮船在B处测得小岛C在北偏东60°方向上,在小岛周围15海里处有暗礁,若轮船仍然按18海里/时的速度向东航行,请问是否有触礁危险?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果“节约10%”记作+10%,那么“浪费6%”记作: .
相关试题

