【题目】如图,P是线段AB上一点,AB=12cm,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上),运动的时间为t.
![]()
(1)当t=1时,PD=2AC,请求出AP的长;
(2)当t=2时,PD=2AC,请求出AP的长;
(3)若C、D运动到任一时刻时,总有PD=2AC,请求出AP的长;
(4)在(3)的条件下,Q是直线AB上一点,且AQ﹣BQ=PQ,求PQ的长.
参考答案:
【答案】(1)4cm;(2)4cm;(3)4cm;(4)4cm或12cm
【解析】试题分析:
(1) 观察图形可以看出,图中的线段PC和线段BD的长分别代表动点C和D的运动路程. 利用“路程等于速度与时间之积”的关系可以得到线段PC和线段BD的长,进而发现BD=2PC. 结合条件PD=2AC,可以得到PB=2AP. 根据上述关系以及线段AB的长,可以求得线段AP的长.
(2) 利用“路程等于速度与时间之积”的关系结合题目中给出的运动时间,可以求得线段PC和线段BD的长,进而发现BD=2PC. 根据BD=2PC和PD=2AC的关系,依照第(1)小题的思路,可以求得线段AP的长.
(3) 利用“路程等于速度与时间之积”的关系可知,只要运动时间一致,点C与点D运动路程的关系与它们运动速度的关系一致. 根据题目中给出的运动速度的关系,可以得到BD=2PC. 这样,本小题的思路就与前两个小题的思路一致了. 于是,依照第(1)小题的思路,可以求得线段AP的长.
(4) 由于题目中没有指明点Q与线段AB的位置关系,所以应该按照点Q在线段AB上以及点Q在线段AB的延长线上两种情况分别进行求解. 首先,根据题意和相关的条件画出相应的示意图. 根据图中各线段之间的关系并结合条件AQ-BQ=PQ,得到AP和BQ之间的关系,借助前面几个小题的结论,即可求得线段PQ的长.
试题解析:
(1) 因为点C从P出发以1(cm/s)的速度运动,运动的时间为t=1(s),所以![]() (cm).
(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t=1(s),所以![]() (cm).
(cm).
故BD=2PC.
因为PD=2AC,BD=2PC,所以BD+PD=2(PC+AC),即PB=2AP.
故AB=AP+PB=3AP.
因为AB=12cm,所以![]() (cm).
(cm).
(2) 因为点C从P出发以1(cm/s)的速度运动,运动的时间为t=2(s),所以![]() (cm).
(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t=2(s),所以![]() (cm).
(cm).
故BD=2PC.
因为PD=2AC,BD=2PC,所以BD+PD=2(PC+AC),即PB=2AP.
故AB=AP+PB=3AP.
因为AB=12cm,所以![]() (cm).
(cm).
(3) 因为点C从P出发以1(cm/s)的速度运动,运动的时间为t(s),所以![]() (cm).
(cm).
因为点D从B出发以2(cm/s)的速度运动,运动的时间为t(s),所以![]() (cm).
(cm).
故BD=2PC.
因为PD=2AC,BD=2PC,所以BD+PD=2(PC+AC),即PB=2AP.
故AB=AP+PB=3AP.
因为AB=12cm,所以![]() (cm).
(cm).
(4) 本题需要对以下两种情况分别进行讨论.
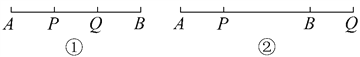
(1) 点Q在线段AB上(如图①).
因为AQ-BQ=PQ,所以AQ=PQ+BQ.
因为AQ=AP+PQ,所以AP=BQ.
因为![]() ,所以
,所以![]() .
.
故![]() .
.
因为AB=12cm,所以![]() (cm).
(cm).
(2) 点Q不在线段AB上,则点Q在线段AB的延长线上(如图②).
因为AQ-BQ=PQ,所以AQ=PQ+BQ.
因为AQ=AP+PQ,所以AP=BQ.
因为![]() ,所以
,所以![]() .
.
故![]() .
.
因为AB=12cm,所以![]() (cm).
(cm).
综上所述,PQ的长为4cm或12cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是BC边上的中点,DE、DF分别垂直AB、AC于点E和F.
求证:DE=DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),∠AOB=120°,在∠AOB内作两条射线OC和OD,且OM平分∠AOD,ON平分∠BOC.
①若∠AOC:∠COD:∠DOB=5:3:4,求∠MON的度数.
②若将图(1)中的∠COD绕点O顺时针转一个小于70°的角α如图(2),其它条件不变,请直接写出∠MON的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)
 ;
;(2)
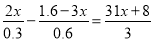 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】物体向右运动4m记作+4m,那么物体向左运动3m,应记作m.
-
科目: 来源: 题型:
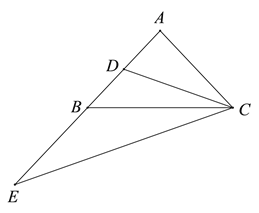
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB至点E,使BE=AB,连接CE. 请你探究:
(1)当∠BAC为直角时,直接写出线段CE与CD之间的数量关系;
(2)当∠BAC为锐角或钝角时,(1)中的上述数量关系是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A. 形状相同的两个三角形是全等形
B. 面积相等的两个三角形全等
C. 周长相等的两个三角形全等
D. 周长相等的两个等边三角形全等
相关试题

