【题目】如图,一艘轮船以18海里/时的速度由西向东航行,在A处测得小岛C在北偏东75°方向上,两小时后,轮船在B处测得小岛C在北偏东60°方向上,在小岛周围15海里处有暗礁,若轮船仍然按18海里/时的速度向东航行,请问是否有触礁危险?并说明理由. 
参考答案:
【答案】解:作CE⊥AB于E,
∵A处测得小岛P在北偏东75°方向,
∴∠CAB=15°,
∵在B处测得小岛P在北偏东60°方向,
∴∠ACB=15°,
∴AB=PB=2×18=36(海里),
∵∠CBD=30°,
∴CE= ![]() BC=18>15,
BC=18>15,
∴船不改变航向,不会触礁.
【解析】作CE⊥AB,利用直角三角形性质求出CE长,和15海里比较即可看出船不改变航向是否会触礁.
【考点精析】解答此题的关键在于理解关于方向角问题的相关知识,掌握指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】物体向右运动4m记作+4m,那么物体向左运动3m,应记作m.
-
科目: 来源: 题型:
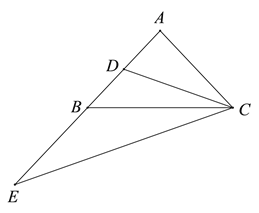
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB至点E,使BE=AB,连接CE. 请你探究:
(1)当∠BAC为直角时,直接写出线段CE与CD之间的数量关系;
(2)当∠BAC为锐角或钝角时,(1)中的上述数量关系是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是( )
A. 形状相同的两个三角形是全等形
B. 面积相等的两个三角形全等
C. 周长相等的两个三角形全等
D. 周长相等的两个等边三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果“节约10%”记作+10%,那么“浪费6%”记作: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数
 的图象与x轴有2个交点.
的图象与x轴有2个交点.(1)求k的取值范围;
(2)若图象与x轴交点的横坐标为
 ,且它们的倒数之和是
,且它们的倒数之和是 ,求k的值.
,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形ABC中,AC=BC,分别以BC和AC为直角边向上作等腰直角三角形△BCD和△ACE,AE与BD相交于点F,连接CF并延长交AB于点G.求证:CG垂直平分AB.

相关试题

