【题目】如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.

参考答案:
【答案】(1)证明见解析;
(2)150°.
【解析】试题分析:
(1)结合等边三角形和正方形的性质,用SAS证明△ABE≌△DCE;
(2)由∠ABE=90°-60°=30°,BA=BE得∠AEB的度数,同理得∠CDE的度数,即可求解.
试题解析:
(1)∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
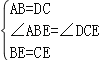 ,
,
∴△ABE≌△DCE(SAS).
(2)∵BA=BE,∠ABE=30°,∴∠BAE=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵∠BAD=90°,∴∠EAD=90°﹣75°=15°,同理可得∠ADE=15°,
∴∠AED=180°﹣15°﹣15°=150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
 ,那么AC=_____.
,那么AC=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】李明准备进行如下操作试验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.



(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)著点P在图(2)位置时,请写出∠1、∠2、∠3之间的关系,并说明理由;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;

(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
【答案】(1)面积等于5(2)图形见解析(3)最小值是根号17
【解析】试题分析:(1)利用勾股定理求出三角形边长,并证明是直角三角形求面积.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.(3)利用对称利用两点之间直线最短求最小值.
试题解析:
(1)分别利用勾股定理求得AC=2
 ,AB=
,AB=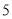 ,BC=
,BC=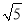 ,
,  ,所以∠ACB=90°,面积等于
,所以∠ACB=90°,面积等于 =5.
=5.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.如下图.

(3)作B点对称B’,连接B’C交DE于P,B’P+PC=BP+CP,所以使PB+PC最小.
利用勾股定理B’C=
 ,
,所以最小值是根号17.

点睛:平面上最短路径问题
(1)归于“两点之间的连线中,线段最短”.凡属于求“变动的两线段之和的最小值”时,大都应用这一模型.
(2)归于“三角形两边之差小于第三边”.凡属于求“变动的两线段之差的最大值”时,大都应用这一模型.
(3)平面图形中,直线同侧两点到直线上一点距离之和最短问题.

【题型】解答题
【结束】
23【题目】已知一次函数y=kx+7的图像经过点A(2,3).
(1)求k的值;
(2)判断点B(-1,8),C(3,1)是否在这个函数的图像上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:①GA=GP;②∠DCP=45°;③BP垂直平分CE;④GF+ FC =GA;其中正确的判断有______________.(填序号)

相关试题

