【题目】如图,Rt△ABC中,∠ACB=90°,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:①GA=GP;②∠DCP=45°;③BP垂直平分CE;④GF+ FC =GA;其中正确的判断有______________.(填序号)

参考答案:
【答案】①②③④;
【解析】①∵AP平分∠BAC,∴∠CAP=∠BAP,
∵PG∥AD,∴∠APG=∠CAP,∴∠APG=∠BAP,∴GA=GP;
②∵AP平分∠BAC,∴P到AC,AB的距离相等,
∵BP平分∠CBE,∴P到BC,AB的距离相等,
∴P到AC,BC的距离相等,
∴CP平分∠BCD,∴∠DCP=45°;
③∵BE=BC,BP平分∠CBE,∴BP垂直平分CE(三线合一);
④∵∠BAC与∠CBE的平分线相交于点P,可得点P也位于∠BCD的平分线上,
∴∠DCP=∠BCP,
又PG∥AD,∴∠FPC=∠DCP,∴FP=FC,
∴GF+FC=GF+FP=GP=AG,
故①②③④都正确,
故答案为:①②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.



(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)著点P在图(2)位置时,请写出∠1、∠2、∠3之间的关系,并说明理由;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;

(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
【答案】(1)面积等于5(2)图形见解析(3)最小值是根号17
【解析】试题分析:(1)利用勾股定理求出三角形边长,并证明是直角三角形求面积.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.(3)利用对称利用两点之间直线最短求最小值.
试题解析:
(1)分别利用勾股定理求得AC=2
 ,AB=
,AB=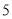 ,BC=
,BC=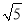 ,
,  ,所以∠ACB=90°,面积等于
,所以∠ACB=90°,面积等于 =5.
=5.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.如下图.

(3)作B点对称B’,连接B’C交DE于P,B’P+PC=BP+CP,所以使PB+PC最小.
利用勾股定理B’C=
 ,
,所以最小值是根号17.

点睛:平面上最短路径问题
(1)归于“两点之间的连线中,线段最短”.凡属于求“变动的两线段之和的最小值”时,大都应用这一模型.
(2)归于“三角形两边之差小于第三边”.凡属于求“变动的两线段之差的最大值”时,大都应用这一模型.
(3)平面图形中,直线同侧两点到直线上一点距离之和最短问题.

【题型】解答题
【结束】
23【题目】已知一次函数y=kx+7的图像经过点A(2,3).
(1)求k的值;
(2)判断点B(-1,8),C(3,1)是否在这个函数的图像上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+7的图像经过点A(2,3).
(1)求k的值;
(2)判断点B(-1,8),C(3,1)是否在这个函数的图像上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
【答案】(1)k=-2(2)点B不在,点C在,(3)9<y<13
【解析】
试题分析:(1)把点A(2,3)代入y=kx+7即可求出k的值;(2)点B(-1,8),C(3,1)的横坐标代入函数解析式验证即可;(3)根据x的取值范围,即可求出y的取值范围.
试题解析:(1)把点A(2,3)代入y=kx+7得:k=-2
(2)当x=-1时,y=-2×(-1)+7=9
∵9≠8∴点B不在抛物线上.
当x=3时,y=-2×3+7=1
∴点C在抛物线上
(3)当x=-3时,y=13,当x=-,1时,y=9,所以9<y<13
考点:一次函数.
【题型】解答题
【结束】
24【题目】顺丰快递公司派甲、乙两车从A地将一批物品匀速运往B地,甲出发0.5h后乙开始出发,结果比甲早1(h)到达B地,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,a表示A、B两地之间的距离.请结合图中的信息解决如下问题:

(1)分别计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回,请问甲车到达B地后以多大的速度立即匀速返回,才能与乙车同时回到A地?并在图中画出甲、乙两车在返回过程中离A地的距离S(km)与时间t(h)的函数图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富居民业余生活,某居民区组建筹委会,该筹委会动员居民自愿集资建立一个书刊阅览室.经预算,一共需要筹资30 000元,其中一部分用于购买书桌、书架等设施,另一部分用于购买书刊.
(1)筹委会计划,购买书刊的资金不少于购买书桌、书架等设施资金的3倍,问最多用多少资金购买书桌、书架等设施?
(2)经初步统计,有200户居民自愿参与集资,那么平均每户需集资150元.镇政府了解情况后,赠送了一批阅览室设施和书籍,这样,只需参与户共集资20 000元.经筹委会进一步宣传,自愿参与的户数在200户的基础上增加了a%(其中a>0).则每户平均集资的资金在150元的基础上减少了
 a%,求a的值.
a%,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )

A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
相关试题

