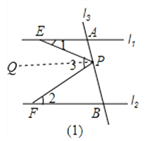
【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.



(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
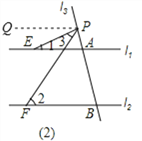
(2)著点P在图(2)位置时,请写出∠1、∠2、∠3之间的关系,并说明理由;
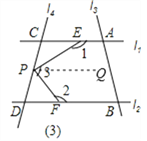
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系
参考答案:
【答案】(1)证明见解析;(2)∠2=∠3+∠1, 理由见解析;(3)∠1+∠2+∠3=360°
【解析】分析:此题三个小题的解题思路是一致的,过P作直线![]() 、
、![]() 的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.
的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.
本题解析:
(1)证明:过点P作PM∥l1 ∵l1∥l2, PM∥l1 ∴PM∥l2
∴∠2=∠FPM ∵PM∥l1 ∴∠1=∠EPM
∴∠3=∠FPM+∠EPM=∠2+∠1
(2)解:∠2=∠3+∠1 理由如下
过点P作PN∥l1 ∵l1∥l2, PN∥l1 ∴PN∥l2
∴∠2=∠FPM ∵PM∥l1 ∴∠1=∠EPM
∴∠2=∠FPM=∠3+∠EPM=∠3+∠1
(3)∠1+∠2+∠3=360°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=
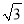 ,求ED的长.
,求ED的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)n边形(n>3)其中一个顶点的对角线有_____条;
(2)一个凸多边形共有14条对角线,它是几边形?
(3)是否存在有21条对角线的凸多边形?如果存在,它是几边形?如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地探空气球的气象观测资料表明,高度每增加1千米,气温下降大约5℃,若该地区地面温度为23℃,该地区高空某点温度为-27℃,则此点的高度是大约是多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连结DF,下列四个结论:①△AEF∽△CAB;②tan∠CAD=
 ;③DF=DC;④CF=2AF,正确的是( )
;③DF=DC;④CF=2AF,正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(答案要求保留小数点后两位数)已知一次考试中某题得分的频数分布表
得分
0分
1分
2分
3分
4分
5分
合计
频数
2
4
6
16
8
6
__
频率
__
__
__
__
__
__
__
(1)完成上面表格;
(2)该题的平均得分是__;得__分的人数最多,占总人数的__%;
(3)将该题的得分情况制作成扇形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有______.
的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有______.
相关试题

