【题目】材料1:一般地,![]() 个相同因数
个相同因数![]() 相乘:
相乘:![]() 记为
记为![]() .如
.如![]() ,此时,3叫做以2为底的8的对数,记为
,此时,3叫做以2为底的8的对数,记为![]() (即
(即![]() )
)
(1)计算![]() __________,
__________,![]() __________.
__________.
材料2:新规定一种运算法则:自然数1到![]() 的连乘积用
的连乘积用![]() 表示,例如:
表示,例如:![]() ,
,![]() ,
,![]() ,
,![]() ,…在这种规定下
,…在这种规定下
(2)求出满足该等式的![]() :
:![]()
(3)当![]() 为何值时,
为何值时,![]()
参考答案:
【答案】(1)2 ,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据材料示例计算可得;
(2)根据材料定义的运算,化简后解含绝对值的方程即可求得;
(3)综合两个材料中的定义,化简后得到解方程可求得.此方程化简后为|x+2|+|x-6|=10,可理解为求数轴上一点x到-2和6的距离之和为10,由-2和6两个点将数轴分为三部分,当x分别位于这三个区域时将方程去绝对值号后进行解方程.
解:(1)由题意可知:log39=2,
(log216)2+![]() log381=42+
log381=42+![]() ×4=
×4=![]() ,
,
故答案为:2;![]() .
.
(2)![]()
化简得:|x-1|=6
即x-1=6或x-1=-6
∴x=7或x=-5
故符合题意的x值为7或-5.
(3)由|x+log416|+|x-3!|=10得|x+2|+|x-6|=10
当x+2=0时,可得x=-2;
当x-6=0时,可得x=6.
则当x<-2时,原方程可化为:-x-2-x+6=10,解得x=-3;
当-2≤x≤6时,原方程可化为:x+2-x+6=10,则此时方程无解;
当x>6时,原方程可化为:x+2+x-6=10,解得x=7.
故当x为-3或7时,符合题意.
-
科目: 来源: 题型:
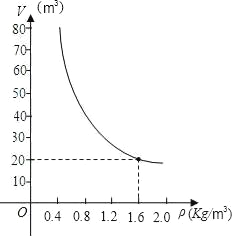
查看答案和解析>>【题目】已知质量一定的某物体的体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图所示:
(1)请写出该物体的体积V与密度ρ的函数关系式;
(2)当该物体的密度ρ=3.2Kg/m3时,它的体积v是多少?
(3)如果将该物体的体积控制在10m3~40m3之间,那么该物体的密度应在什么范围内变化?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,点B是
,点B是 的中点,且
的中点,且 ,
, .
.
(1)若AE=25,CE=14,求△ACE的面积;
(2)求证:四边形ABCD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系?加以证明;
(2)若∠CEF=70°,求∠ACB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.

(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?
(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.
 B.
B. 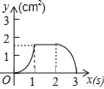 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将挂好彩旗的旗杆垂直插在操场上,旗杆从旗顶到地面的高度为320cm,在无风的天气里,彩旗自然下垂,如图所示,
(1)求彩旗下垂时最低处离地面的最小高度h.彩旗完全展平时的尺寸如图的长方形(单位:cm)
(2)商店彩旗的标价为每面40元,旗杆的标价为每根20元,学校计划购买彩旗60面,旗杆50根,由于数量较多商店决定给予学校优惠,其中彩旗每面优惠10%,旗杆每根优惠
 a%,这样,学校彩旗又多购买了2a%,旗杆的数量不变,这样总共花费3542元,求a的值.
a%,这样,学校彩旗又多购买了2a%,旗杆的数量不变,这样总共花费3542元,求a的值.
相关试题

