【题目】如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°,
(1)问直线EF与AB有怎样的位置关系?加以证明;
(2)若∠CEF=70°,求∠ACB的度数.

参考答案:
【答案】(1)EF和AB的关系为平行关系;(2)∠ACB=40°.
【解析】
(1)由平行线的性质推出∠DCB=∠ABC=70°,结合∠CBF=20°,推出∠ABF=50°,即可得出∠EFB+∠ABF=180°,根据平行线的判定即可推出EF∥AB;
(2)根据(1)推出的结论,推出EF∥CD,根据平行线的性质推出∠ECD=110°,根据∠DCB=70°,即可求出∠ACB的度数.
解:(1)EF和AB的关系为平行关系.理由如下:
∵CD∥AB,∠DCB=70°,
∴∠DCB=∠ABC=70°,
∵∠CBF=20°,
∴∠ABF=∠ABC﹣∠CBF=50°,
∵∠EFB=130°,
∴∠ABF+∠EFB=50°+130°=180°,
∴EF∥AB;
(2)∵EF∥AB,CD∥AB,
∴EF∥CD,
∵∠CEF=70°,
∴∠ECD=110°,
∵∠DCB=70°,
∴∠ACB=∠ECD﹣∠DCB,
∴∠ACB=40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小莉的家在锦江河畔的电梯公寓AD内,她家的河对岸新建了一座大厦BC,为了测量大厦的高度,小莉在她家的楼底A处测得大厦顶部B的仰角为60°,爬上楼顶D处测得大厦顶部B的仰角为30°,已知电梯公寓高82米,请你帮助小莉计算出大厦的高度BC及大厦与电梯公寓间的距离AC.
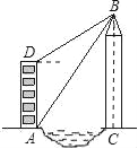
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知质量一定的某物体的体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图所示:
(1)请写出该物体的体积V与密度ρ的函数关系式;
(2)当该物体的密度ρ=3.2Kg/m3时,它的体积v是多少?
(3)如果将该物体的体积控制在10m3~40m3之间,那么该物体的密度应在什么范围内变化?
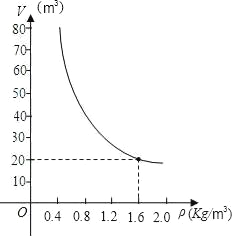
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,点B是
,点B是 的中点,且
的中点,且 ,
, .
.
(1)若AE=25,CE=14,求△ACE的面积;
(2)求证:四边形ABCD是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】材料1:一般地,
 个相同因数
个相同因数 相乘:
相乘: 记为
记为 .如
.如 ,此时,3叫做以2为底的8的对数,记为
,此时,3叫做以2为底的8的对数,记为 (即
(即 )
)(1)计算
 __________,
__________, __________.
__________.材料2:新规定一种运算法则:自然数1到
 的连乘积用
的连乘积用 表示,例如:
表示,例如: ,
, ,
, ,
, ,…在这种规定下
,…在这种规定下(2)求出满足该等式的
 :
:
(3)当
 为何值时,
为何值时,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点. 连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.

(1)求证:△APE∽△ADQ;
(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?
(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必给出证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.
 B.
B. 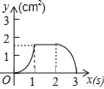 C.
C.  D.
D. 
相关试题

