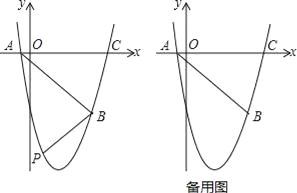
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点 经过点A（﹣1，0），B（5，﹣6），C（6，0）

（1）求抛物线的解析式；

（2）如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；

（3）若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？并请求出其中某一个点Q的坐标.

参考答案：

【答案】（1）y=x2﹣5x﹣6；（2）存在，P（2，﹣12）；（3）Q点一共有5个，（，﹣）．

【解析】试题分析：（1）抛物线经过点A（﹣1，0），B（5，﹣6），C（6，0），可利用两点式法设抛物线的解析式为y=a（x+1）（x﹣6），代入B（5，﹣6）即可求得函数的解析式；（2）作辅助线，将四边形PACB分成三个图形，两个三角形和一个梯形，设P（m，m2﹣5m﹣6），四边形PACB的面积为S，用字母m表示出四边形PACB的面积S，发现是一个二次函数，利用顶点坐标求极值，从而求出点P的坐标．（3）分三种情况画图：①以A为圆心，AB为半径画弧，交对称轴于Q1和Q4，有两个符合条件的Q1和Q4；②以B为圆心，以BA为半径画弧，也有两个符合条件的Q2和Q5；③作AB的垂直平分线交对称轴于一点Q3，有一个符合条件的Q3；最后利用等腰三角形的腰相等，利用勾股定理列方程求出Q3坐标．

试题解析：（1）设y=a（x+1）（x﹣6）（a≠0），

把B（5，﹣6）代入：a（5+1）（5﹣6）=﹣6，

a=1，

∴y=（x+1）（x﹣6）=x2﹣5x﹣6；

（2）存在，

如图1，分别过P、B向x轴作垂线PM和BN，垂足分别为M、N，

设P（m，m2﹣5m﹣6），四边形PACB的面积为S，

则PM=﹣m2+5m+6，AM=m+1，MN=5﹣m，CN=6﹣5=1，BN=5，

∴S=S△AMP+S梯形PMNB+S△BNC

=（﹣m2+5m+6）（m+1）+（6﹣m2+5m+6）（5﹣m）+×1×6

=﹣3m2+12m+36

=﹣3（m﹣2）2+48，

当m=2时，S有最大值为48，这时m2﹣5m﹣6=22﹣5×2﹣6=﹣12，

∴P（2，﹣12），

（3）这样的Q点一共有5个，连接Q3A、Q3B，

y=x2﹣5x﹣6=（x﹣）2﹣；

因为Q3在对称轴上，所以设Q3（，y），

∵△Q3AB是等腰三角形，且Q3A=Q3B，

由勾股定理得：（+1）2+y2=（﹣5）2+（y+6）2，

y=﹣，

∴Q3（，﹣）．

关闭