【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲乙两地之间的距离为______千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.

参考答案:
【答案】(1)560;(2)快车:80km/h;慢车:60km/h;(3)y=﹣60x+540(8≤x≤9)
【解析】试题分析:(1)根据函数图象直接得出答案;(2)根据题意得出:慢车往返分别用了4小时,慢车行驶4小时的距离,快车3小时即可行驶完,然后设慢车速度为3xkm/h,快车速度为4xkm/h,从而得出答案;(3)分别根据图象以及所求的速度得出点D和点E的坐标.然后利用待定系数法求出函数解析式.
试题解析:(1)由题意可得出:甲乙两地之间的距离为560千米;
(2)由题意可得出:慢车往返分别用了4小时,慢车行驶4小时的距离,快车3小时即可行驶完,
∴设慢车速度为3xkm/h,快车速度为4xkm/h, ∵由题意可得出:快车行驶全程用了7小时,
∴快车速度为:![]() =80(km/h), ∴4x=80 ∴x=20 ∴慢车速度为:3x=3×20=60(km/h),
=80(km/h), ∴4x=80 ∴x=20 ∴慢车速度为:3x=3×20=60(km/h),
(3)由题意可得出:当行驶7小时后,慢车距离甲地60km, ∴D(8,60)
∵慢车往返各需4小时, ∴E(9,0), 设DE的解析式为:y=kx+b,
∴![]() , 解得:
, 解得:![]() .
.
∴线段DE所表示的y与x之间的函数关系式为:y=﹣60x+540(8≤x≤9).
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.

(1)请用两种不同的方法求图2中阴影部分的面积(直接用含m,n的代数式表示) 方法1:
方法2:
(2)根据(1)中结论,请你写出下列三个代数式之间的等量关系;代数式:(m+n)2 , (m﹣n)2 , mn
(3)根据(2)题中的等量关系,解决如下问题:已知a+b=8,ab=7,求a﹣b和a2﹣b2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点 经过点A(﹣1,0),B(5,﹣6),C(6,0)
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
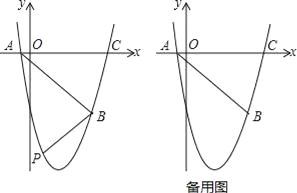
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知七名选手参加演讲比赛,所得分数各不同.其中一名选手想知道自己能否进入前四名,他除了知道他本人的分数外,还要知道七名选手分数的( )
A. 中位数B. 众数C. 平均数D. 方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )

A.
B.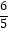
C.
D.不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】近似数4.50所表示的准确值a的取值范围是( )
A.4.495≤a<4.505
B.4040≤a<4.60
C.4.495≤a≤4.505
D.4.500≤a<4.5056
相关试题

