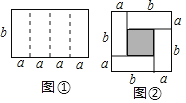
【题目】如图①是一个长为4a、宽为b的长方形,沿图中虚线用剪刀将其平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②)
自主探索:
(1)仔细观察图形,完成下列问题
①图②中的阴影部分的面积为_____;
②观察图②,请你写出(a+b)2、(a-b)2、ab之间的等量关系是_____;
知识运用:
(2)若x-y=5,xy=![]() ,根据(1)中的结论,求(x+y)2的值;
,根据(1)中的结论,求(x+y)2的值;
知识延伸
(3)根据你探索发现的结论,完成下列问题:
设A=![]() ,B=x+2y-3
,B=x+2y-3
计算(A-B)2-(A+B)2的结果.
参考答案:
【答案】(1)①阴影部分的面积为(b-a)2,②(a+b)2=(b-a)2+4ab;(2)36;(3)4y2-x2+6x-9.
【解析】
(1)①阴影部分面积直接利用边长乘边长即可 ②利用正方形面积等于空白部分面积加上阴影部分面积即可 (2)(x+y)2=(x-y)2+4xy代入求值即可 (3)(A-B)2-(A+B)2= A2-2AB+B2-A2-2AB-B2=-4AB,代入A、B计算即可
(1)①图②中的阴影部分的面积为(b-a)2,
②由图2知,(a+b)2、(a-b)2、ab之间的等量关系是(a+b)2=(b-a)2+4ab,即(a+b)2=(a-b)2+4ab,
故答案为:(b-a)2、(a+b)2=(b-a)2+4ab;
(2)(x+y)2=(x-y)2+4xy
=52+4×![]()
=25+11
=36;
(3)当A=![]() ,B=x+2y-3时,
,B=x+2y-3时,
原式=A2-2AB+B2-A2-2AB-B2
=-4AB
=-4×![]() ×(x+2y-3)
×(x+2y-3)
=-(x-2y-3)(x+2y-3)
=-[(x-3)2-4y2]
=-(x2-6x+9-4y2)
=4y2-x2+6x-9.
-
科目: 来源: 题型:
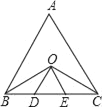
查看答案和解析>>【题目】如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果把一个自然数各数位上数字从最高位到个位依次排出一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数叫做 “和谐数”.例如:自然数64746从最高位到个位排出的一串数字是:6、4、7、4、6,从个位到最高排出的一串数字也是:6、4、7、4、6,所64746是“和谐数”.再如:33,181,212,4664,…,都是“和谐数”.
(1)请你直接写出3个四位“和谐数”,猜想任意一个四位“和谐数”能否被11整除,并说明理由;[来。
(2) 已知一个能被11整除的三位“和谐数”,设个位上的数字为x(
 ,x为自然数),十位上的数字为y,求y与x的函数关系式.
,x为自然数),十位上的数字为y,求y与x的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】将正面分别标有数字1、2、3的三张卡片洗匀后,背面朝上放在桌面上请完成下列各题
(1)随机抽取1张,求抽到卡片数字是奇数的概率;
(2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?
(3)在(2)的条件下,试求组成的两位数是偶数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
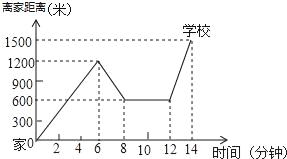
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以点P(﹣1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2,将△ABC绕点P旋转180°,得到△MCB.
(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.

相关试题

