【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OD,由切线的性质即可得出∠ODF=90°,再由BD=CD,OA=OB可得出OD是△ABC的中位线,根据三角形中位线的性质即可得出,根据平行线的性质即可得出∠CFD=∠ODF=90°,从而证出DF⊥AC;
(2)由∠CDF=30°以及∠ODF=90°即可算出∠ODB=60°,再结合OB=OD可得出△OBD是等边三角形,根据弧长公式即可得出结论.
试题解析:(1)证明:连接OD,如图所示.∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.
∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,∴∠CFD=∠ODF=90°,∴DF⊥AC.
(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,∴![]() 的长=
的长=![]() =
=![]() =
=![]() .
.

-
科目: 来源: 题型:
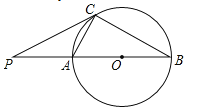
查看答案和解析>>【题目】如图,已知⊙O的直径AB=12cm,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
(1)求证:∠PCA=∠B;
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣2)3﹣( )﹣1+(
)﹣1+( 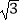 ﹣1)0+(﹣
﹣1)0+(﹣  )2017×(1.5)2016
)2017×(1.5)2016
(2)(2a+1)(2a﹣1)﹣(a+2)2﹣3a(a+1)
(3)(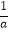 ﹣1)÷
﹣1)÷ 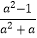 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )
A.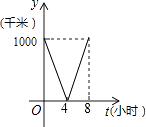
B.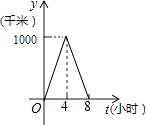
C.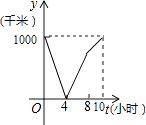
D.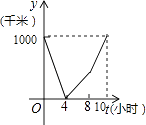
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(1,a)和点N(﹣2,b)是一次函数y=﹣3x+1图象上的两点,则a与b的大小关系是_____.
-
科目: 来源: 题型:
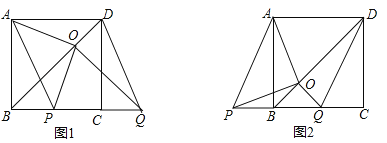
查看答案和解析>>【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=x+2的图象经过点A(a,b),B(c,d),那么ac﹣ad﹣bc+bd的值为__.
相关试题

