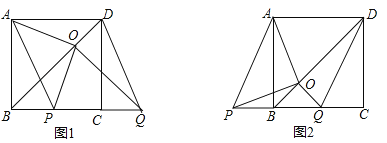
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.
参考答案:
【答案】(1)四边形APQD为平行四边形;(2)OA=OP,OA⊥OP;(3)当P点在B点右侧时, y=![]() ;当P点在B点左侧时, y=
;当P点在B点左侧时, y=![]() ;当x=2时,y有最大值为2.
;当x=2时,y有最大值为2.
【解析】
试题分析:(1)四边形APQD为平行四边形;
(2)OA=OP,OA⊥OP,理由如下:
∵四边形ABCD是正方形,∴AB=BC=PQ,∠ABO=∠OBQ=45°,∵OQ⊥BD,∴∠PQO=45°,∴∠ABO=∠OBQ=∠PQO=45°,∴OB=OQ,在△AOB和△OPQ中,∵AB=PQ,∠ABO=∠PQO,BO=QO,∴△AOB≌△OPQ(SAS),∴OA=OP,∠AOB=∠PQO,∴∠AOP=∠BOQ=90°,∴OA⊥OP;
(3)如图,过O作OE⊥BC于E.
①如图1,当P点在B点右侧时,则BQ=x+2,OE=![]() ,∴y=
,∴y=![]() ×
×![]() x=
x=![]() ,即
,即![]() ,又∵0≤x≤2,∴当x=2时,y有最大值为2;
,又∵0≤x≤2,∴当x=2时,y有最大值为2;
②如图2,当P点在B点左侧时,则BQ=2﹣x,OE=![]() ,∴y=
,∴y=![]() ×
×![]() x=
x=![]() ,即
,即![]() ,又∵0≤x≤2,∴当x=1时,y有最大值为
,又∵0≤x≤2,∴当x=1时,y有最大值为![]() ;
;
综上所述,当P点在B点右侧时, y=![]() ;当P点在B点左侧时, y=
;当P点在B点左侧时, y=![]() ;
;
∴当x=2时,y有最大值为2;

-
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为100千米/小时,特快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与快车行驶时间(小时)之间的函数图象是( )
A.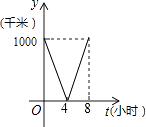
B.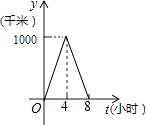
C.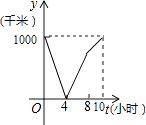
D.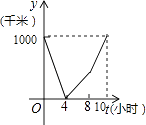
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求
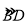 的长(结果保留π).
的长(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(1,a)和点N(﹣2,b)是一次函数y=﹣3x+1图象上的两点,则a与b的大小关系是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=x+2的图象经过点A(a,b),B(c,d),那么ac﹣ad﹣bc+bd的值为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)
(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径
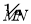 的长度.(结果保留π)
的长度.(结果保留π)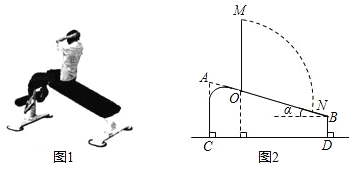
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC在平面直角坐标系中,点A、B、C都在第一象限内,现将△ABC的三个顶点的横坐标保持不变,纵坐标都乘-1,得到一个新的三角形,则( )。
A. 新三角形与△ABC关于x轴对称 B. 新三角形与△ABC关于y轴对称
C. 新三角形的三个顶点都在第三象限内 D. 新三角形是由△ABC沿y轴向下平移一个单位长度得到的
相关试题

