【题目】一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需的最少费用是 .
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
参考答案:
【答案】27
【解析】解:设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为![]() 个,
个,
①当0![]() x<3时,y=5x+
x<3时,y=5x+![]()
![]() 6=x+30,
6=x+30,
∵k=1>0,
∴y随x的增大而增大,
∴当x=0时,y有最小值,最小值为30元.
②当3![]() x
x![]() 6时,y=5x+
6时,y=5x+![]()
![]() 6-1.5x=30-0.5x,
6-1.5x=30-0.5x,
∵k=-0.5<0,
∴y随x的增大而减小,
∴当x=6时,y有最小值,最小值为27元.
综合①②可得,购买盒子所需要最少费用为27元.
故答案为27.
本题考查了列代数式以及一次函数的性质,分0![]() x<3时和3
x<3时和3![]() x
x![]() 6时两种情况,找出y关于x的函数关系式是解题的关键.
6时两种情况,找出y关于x的函数关系式是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列分式方程:
(1)
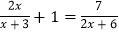 ;
;(2)
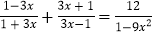 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】两组数据:3,a,2b,5与a,6,b的平均数都是8,若将这两组数据合并为一组数据.
(1)求出a,b的值;
(2)求这组数据的众数和中位数.
-
科目: 来源: 题型:
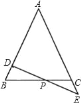
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,D为AB上一点,E为AC延长线上的一点,且CE=BD,连接DE交BC于点P.
(1)求证:PE=PD;
(2)若CE:AC=1:5,BC=10,求BP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正两位数的个位数字是a,十位数字比个位数字大2.
(1)列式表示这个两位数;
(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被22整除.
相关试题

