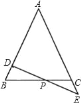
【题目】如图所示,在△ABC中,AB=AC,D为AB上一点,E为AC延长线上的一点,且CE=BD,连接DE交BC于点P.
(1)求证:PE=PD;
(2)若CE:AC=1:5,BC=10,求BP的长.
参考答案:
【答案】(1)见解析;(2)6.
【解析】
(1)过点D作DF∥AC交BC于点F,根据平行线的性质可得:∠ACB=∠DFB,∠FDP=∠E,根据AB=AC,可得∠ACB=∠ABC,进而可得∠ABC=∠DFB,因此DF=DB,再根据CE=BD,可得CE=DF,根据∠DPF=∠CPE,利用全等三角形的判定定理可得:△ECP≌△DFP,根据全等三角形性质可得PE=PD,
(2)根据CE=BD,AC=AB,CE:AC=1:5,可得BD:AB=1:5,
根据DF∥AC,可证得△BDF∽△BAC,根据相似三角形的性质可得![]() ,
,
由BC=10,代入上式可得BF=2,FC=8,根据△DFP≌△ECP,可得FP=PC,因此PF=4,继而可得BP=BF+FP=6.
(1)证明:过点D作DF∥AC交BC于点F,
∴∠ACB=∠DFB,∠FDP=∠E,
∵AB=AC(已知),
∴∠ACB=∠ABC,
∴∠ABC=∠DFB,
∴DF=DB,
又∵CE=BD(已知),
∴CE=DF,
又∵∠DPF=∠CPE,
∴△ECP≌△DFP,
∴PE=PD,
(2)解:∵CE=BD,AC=AB,CE:AC=1:5(已知),
∴BD:AB=1:5,
∵DF∥AC,
∴△BDF∽△BAC,
∴![]() ,
,
∵BC=10,
∴BF=2,FC=8,
∵△DFP≌△ECP,
∴FP=PC,
∴PF=4,
则BP=BF+FP=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于代数式x2-10x+24,下列说法:①它是二次三项式; ②该代数式的值可能等于2017;③分解因式的结果是(x-4)(x-6);④该代数式的值可能小于-1.其中正确的有( )
A.1个
B.2个
C.3 个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列分式方程:
(1)
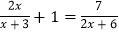 ;
;(2)
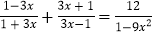 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】两组数据:3,a,2b,5与a,6,b的平均数都是8,若将这两组数据合并为一组数据.
(1)求出a,b的值;
(2)求这组数据的众数和中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需的最少费用是 .
型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.

相关试题

