【题目】给出下列命题:
①三角形的三条高相交于一点;
②如果一组数据中有一个数据变动,那么它的平均数、众数、中位数都随之变动;
③如果不等式![]() 的解集为
的解集为![]() ,那么
,那么![]() ;
;
④如果三角形的一个外角等于与它相邻的一个内角则这个三角形是直角三角形;
其中正确的命题有( )
A.1个B.2个C.3个D.4个
参考答案:
【答案】B
【解析】
根据三角形的高、平均数、众数、中位数的定义、不等式的基本性质和邻补角的定义逐一判断即可.
①钝角三角形的三条高不相交(三条高所在的直线交于一点),故错误;
②如果一组数据中有一个数据变动,那么它的平均数会随之变动,但众数和中位数不一定变动,故错误;
③如果不等式![]() 的解集为
的解集为![]() ,可得m-3<0,那么
,可得m-3<0,那么![]() ,故正确;
,故正确;
④如果三角形的一个外角等于与它相邻的一个内角,根据邻补角的定义可得这个外角和与它相邻的一个内角之和为180°,
∴三角形的这个内角为180°÷2=90°
则这个三角形是直角三角形,故正确.
综上:正确的有2个
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点都在网格点上,建立如图所示的平面直角坐标系.
(1)请根据如图所示的平面直角坐标系,写出△ABC各点的坐标,并求出△ABC的面积.
(2)把△ABC平移到△A1B1C1,使点B1与原点O重合,按要求画出△A1B1C1,并写出平移过程.
(3)已知P是△ABC内有一点,平移至△A1B1C1后,P点对应点的坐标为P1 (a,b),试写出P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交OG于点H.

(1)求证:∠DAE=∠DCG.
(2)求线段HE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,点A在x轴上,直线OC上所有的点坐标
 ,都是二元一次方程
,都是二元一次方程 的解,直线AC上所有的点坐标
的解,直线AC上所有的点坐标 ,都是二元一次方程
,都是二元一次方程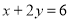 的解,过C作x轴的平行线,交y轴与点B.
的解,过C作x轴的平行线,交y轴与点B.(1)求点A、B、C的坐标;
(2)如图②,点M、N分别为线段BC,OA上的两个动点,点M从点C以每秒1个单位长度的速度向左运动,同时点N从点O以每秒1.5个单位长度的速度向右运动,设运动时间为t秒,且0<t<4,试比较四边形MNAC的面积与四边形MNOB的面积的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )

A. 4 B. 5 C. 6 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(6,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂。”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少。
小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树。他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约_______千米。
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米。小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:

考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值。
相关试题

