【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数 ![]() ,当x=1时,y=3;当x=3时,y=1,即当
,当x=1时,y=3;当x=3时,y=1,即当 ![]() 时,有
时,有 ![]() ,所以说函数
,所以说函数 ![]() 是闭区间[1,3]上的“闭函数”.
是闭区间[1,3]上的“闭函数”.
(1)反比例函数y= ![]() 是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y= ![]() 是闭区间[1,2]上的“闭函数”,求k的值;
是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的表达式(用含m,n的代数式表示).
参考答案:
【答案】
(1)解:反比例函数y= ![]() 是闭区间[1,2016]上的“闭函数”.
是闭区间[1,2016]上的“闭函数”.
理由如下:
反比例函数y= ![]() 在第一象限,y随x的增大而减小,
在第一象限,y随x的增大而减小,
当x=1时,y=2016; 当x=2016时,y=1,
即图象过点(1,2016)和(2016,1)
∴当1≤x≤2016时,有1≤y≤2016,符合闭函数的定义,
∴反比例函数y= ![]() 是闭区间[1,2016]上的“闭函数”
是闭区间[1,2016]上的“闭函数”
(2)解:由于二次函数 ![]() 的图象开口向上,
的图象开口向上,
对称轴为 ![]() ,
,
∴二次函数 ![]() 在闭区间[1,2]内,y随x的增大而增大.
在闭区间[1,2]内,y随x的增大而增大.
当x=1时,y=1,
∴k= ![]() .
.
当x=2时,y=2,
∴k= ![]() .
.
即图象过点(1,1)和(2,2)
∴当1≤x≤2时,有1≤y≤2,符合闭函数的定义,
∴k= ![]()
(3)解:因为一次函数 ![]() 是闭区间
是闭区间 ![]() 上的“闭函数”,
上的“闭函数”,
根据一次函数的图象与性质,有:
(Ⅰ)当 ![]() 时,即图象过点(m,m)和(n,n)
时,即图象过点(m,m)和(n,n)
![]() ,
,
解得 ![]() .
.
∴ ![]()
(Ⅱ)当 ![]() 时,即图象过点(m,n)和(n,m)
时,即图象过点(m,n)和(n,m)
![]() ,解得
,解得 ![]()
∴ ![]() ,
,
∴一次函数的表达式为 ![]() 或
或 ![]()
【解析】(1)根据反比例函数y=![]() 在第一象限,y随x的增大而减小,当x=1时,y=2016;当x=2016时,y=1,即图象过点(1,2016)和(2016,1);当1≤x≤2016时,有1≤y≤2016,符合闭函数的定义,得到反比例函数y=
在第一象限,y随x的增大而减小,当x=1时,y=2016;当x=2016时,y=1,即图象过点(1,2016)和(2016,1);当1≤x≤2016时,有1≤y≤2016,符合闭函数的定义,得到反比例函数y=![]() 是闭区间[1,2016]上的“闭函数”;(2)由于二次函数 y=x22xk的图象开口向上,对称轴为
是闭区间[1,2016]上的“闭函数”;(2)由于二次函数 y=x22xk的图象开口向上,对称轴为![]() ,二次函数
,二次函数![]() 在闭区间[1,2]内,y随x的增大而增大;当x=1时,y=1,k=
在闭区间[1,2]内,y随x的增大而增大;当x=1时,y=1,k= ![]() ;当x=2时,y=2,k=
;当x=2时,y=2,k= ![]() ;即图象过点(1,1)和(2,2)当1≤x≤2时,有1≤y≤2,符合闭函数的定义,求出k的值;(3)根据一次函数的图象与性质,当k>0时,得到y=x;当k<0时,得到y=-x+m+n,得到一次函数的表达式.
;即图象过点(1,1)和(2,2)当1≤x≤2时,有1≤y≤2,符合闭函数的定义,求出k的值;(3)根据一次函数的图象与性质,当k>0时,得到y=x;当k<0时,得到y=-x+m+n,得到一次函数的表达式.![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边
是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边 .
. 如图
如图 ,点D在线段BC上移动时,直接写出
,点D在线段BC上移动时,直接写出 和
和 的大小关系;
的大小关系; 如图
如图 图
图 ,点D在线段BC的延长线上或反向延长线上移动时,猜想
,点D在线段BC的延长线上或反向延长线上移动时,猜想 的大小是否发生变化,若不变请直接写出结论并选择其中一种图示进行证明;若变化,请分别写出图
的大小是否发生变化,若不变请直接写出结论并选择其中一种图示进行证明;若变化,请分别写出图 、图
、图 所对应的结论.
所对应的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.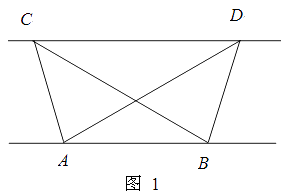
(2)结论应用:① 如图2,点M,N在反比例函数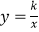 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF. 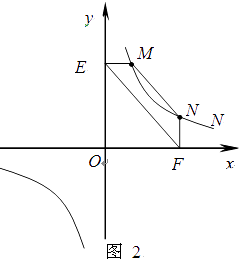
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.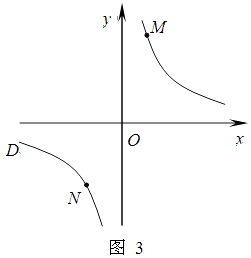
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.
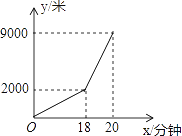
-
科目: 来源: 题型:
查看答案和解析>>【题目】在综合与实践课上,同学们以“一个含
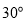 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线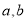 且
且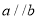 和直角三角形
和直角三角形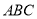 ,
,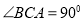 ,
,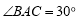 ,
,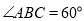 .
.操作发现:
(1)在如图1中,
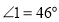 ,求
,求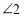 的度数;
的度数;(2)如图2,创新小组的同学把直线
 向上平移,并把
向上平移,并把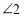 的位置改变,发现
的位置改变,发现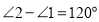 ,说明理由;
,说明理由;实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,
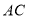 平分
平分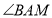 ,此时发现
,此时发现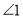 与
与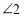 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出 与
与 的数量关系.
的数量关系.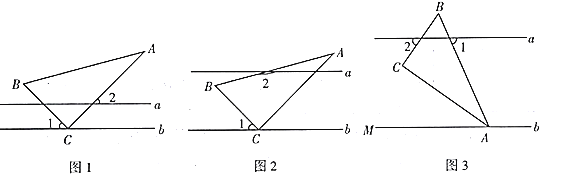
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形纸片ABCD的边长为3,点E,F分别在边BC、CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )

A.1.5
B.2.5
C.2.25
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
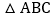 中,
中,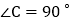 ,
,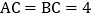 ,D是AB的中点,点E、F分别在AC、BC边上运动
,D是AB的中点,点E、F分别在AC、BC边上运动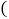 点E不与点A、C重合
点E不与点A、C重合 ,且保持
,且保持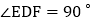 ,连接DE、DF、
,连接DE、DF、 在此运动变化的过程中,有下列结论:
在此运动变化的过程中,有下列结论: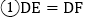 ;
; 四边形CEDF的面积随点E、F位置的改变而发生变化;
四边形CEDF的面积随点E、F位置的改变而发生变化;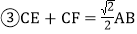 ;
;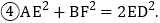 以上结论正确的是______
以上结论正确的是______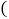 只填序号
只填序号 .
.
相关试题

