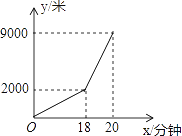
【题目】小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.
参考答案:
【答案】63![]()
【解析】
根据图表可计算出上坡的速度以及下坡的速度,又已知返回途中的上下坡的路程正好相反,故可计算出共用的时间.
由图可得,去校时,上坡路的距离为2000米,所用时间为18分,
∴上坡速度=2000÷18=![]() 米/分,
米/分,
下坡路的距离是9000-2000=7000米,所用时间为20-18=2分,
∴下坡速度=7000÷2=3500米/分;
∵去学校时的上坡回家时变为下坡、去学校时的下坡回家时变为上坡,
∴小明从学校骑车回家用的时间是:7000÷![]() +2000÷3500=63+
+2000÷3500=63+![]() =63
=63![]() 分钟.
分钟.
故答案为:63![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在《科学》课上,老师讲到温度计的使用方法及液体的沸点时,好奇的王红同学准备测量食用油的沸点,已知食用油的沸点温度高于水的沸点温度(
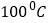 ),王红家只有刻度不超过
),王红家只有刻度不超过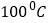 的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔
的温度计,她的方法是在锅中倒入一些食用油,用煤气灶均匀加热,并每隔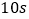 测量一次锅中油温,测量得到的数据如下表:
测量一次锅中油温,测量得到的数据如下表:时间
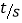
0
10
20
30
40
油温
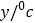
10
30
50
70
90
王红发现,烧了
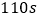 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )A. 没有加热时,油的温度是
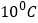
B. 加热
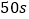 ,油的温度是
,油的温度是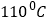
C. 估计这种食用油的沸点温度约是
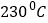
D. 每加热
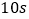 ,油的温度升高
,油的温度升高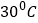
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边
是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边 .
. 如图
如图 ,点D在线段BC上移动时,直接写出
,点D在线段BC上移动时,直接写出 和
和 的大小关系;
的大小关系; 如图
如图 图
图 ,点D在线段BC的延长线上或反向延长线上移动时,猜想
,点D在线段BC的延长线上或反向延长线上移动时,猜想 的大小是否发生变化,若不变请直接写出结论并选择其中一种图示进行证明;若变化,请分别写出图
的大小是否发生变化,若不变请直接写出结论并选择其中一种图示进行证明;若变化,请分别写出图 、图
、图 所对应的结论.
所对应的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.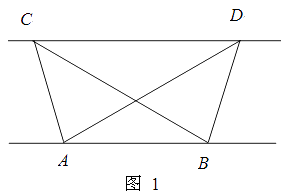
(2)结论应用:① 如图2,点M,N在反比例函数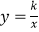 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试证明:MN∥EF. 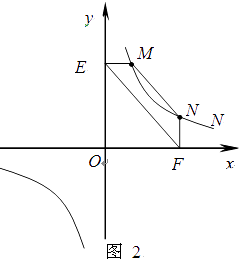
② 若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断 MN与EF是否平行?请说明理由.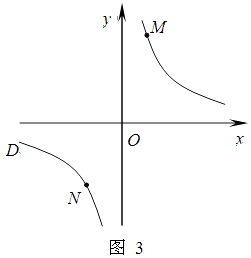
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数
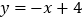 ,当x=1时,y=3;当x=3时,y=1,即当
,当x=1时,y=3;当x=3时,y=1,即当 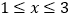 时,有
时,有  ,所以说函数
,所以说函数 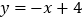 是闭区间[1,3]上的“闭函数”.
是闭区间[1,3]上的“闭函数”.
(1)反比例函数y= 是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y= 是闭区间[1,2]上的“闭函数”,求k的值;
是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的表达式(用含m,n的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】在综合与实践课上,同学们以“一个含
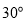 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线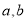 且
且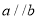 和直角三角形
和直角三角形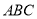 ,
,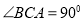 ,
,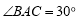 ,
,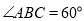 .
.操作发现:
(1)在如图1中,
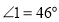 ,求
,求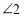 的度数;
的度数;(2)如图2,创新小组的同学把直线
 向上平移,并把
向上平移,并把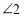 的位置改变,发现
的位置改变,发现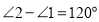 ,说明理由;
,说明理由;实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,
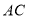 平分
平分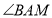 ,此时发现
,此时发现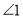 与
与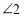 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出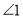 与
与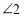 的数量关系.
的数量关系.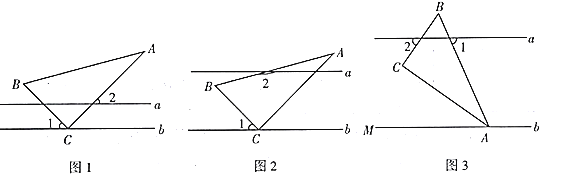
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形纸片ABCD的边长为3,点E,F分别在边BC、CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )

A.1.5
B.2.5
C.2.25
D.3
相关试题

