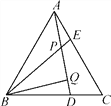
【题目】如图,等边△ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q.
(1)求证:BP=2PQ;
(2)若PE=1,PQ=3,试求AD的长.
参考答案:
【答案】(1)见解析;(2)7
【解析】试题分析:![]() 根据全等三角形的判定方法SAS可证得△BEC≌△ADB,根据各角的关系及三角形内角、外角和定理可证得
根据全等三角形的判定方法SAS可证得△BEC≌△ADB,根据各角的关系及三角形内角、外角和定理可证得![]() ,即可得结论.
,即可得结论.
![]() 由已知条件,先证明△ABE≌△CAD得
由已知条件,先证明△ABE≌△CAD得![]() ,可得
,可得![]() .即可求出
.即可求出![]() 的长.
的长.
试题解析:
![]() AE=CD,AC=BC,
AE=CD,AC=BC,
∴EC=BD;
∵△ABC为等边三角形,
![]()
在△BEC与△ADB中,
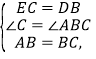
∴△BEC≌△ADB(SAS),
∴∠EBC=∠BAD;
∵∠ABE+∠EBC=![]() ,则∠ABE+∠BAD=
,则∠ABE+∠BAD=![]() ,
,
∵∠BPQ是△ABP外角,
∴∠ABP+∠BAP=![]() =∠BPQ,
=∠BPQ,
又∵BQ⊥AD,
![]()
∴BP=2PQ.
![]() ∵△ABC为等边三角形,
∵△ABC为等边三角形,
∴AB=CA,∠BAE=∠ACD=![]() ;
;
又∵AE=CD,
在△ABE和△CAD中,
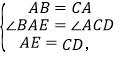
∴△ABE≌△CAD(SAS);
∴BE=AD,∠CAD=∠ABE;
![]()
∵BQ⊥AD,
![]() ,则
,则![]()
∵PQ=3,
∴在Rt△BPQ中,BP=2PQ=6;
又∵PE=1,
∴AD=BE=BP+PE=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市进行“新城区改造建设”,有甲、乙两种车参加运土,已知5辆甲种车和2辆乙种车一次共可运土64米
 ,3辆甲种车和1辆乙种车一次共可运土36米
,3辆甲种车和1辆乙种车一次共可运土36米 .
.(1)求甲、乙两种车每辆一次可分别运土多少米
 ;
;(2)某公司派甲、乙两种汽车共10辆参加运土,且一次运土总量不低于100米
 ,求公司最多要派多少辆甲种汽车参加运土.
,求公司最多要派多少辆甲种汽车参加运土. -
科目: 来源: 题型:
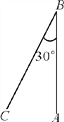
查看答案和解析>>【题目】台风是一种自然灾害,如图,气象部门观测到距离A市正北方向200千米的B处有一台风中心,其中心最大风力为12级,该台风中心正以18千米/时的速度沿直线向C移动,且台风中心风力不变,已知每远离台风中心20千米,风力就减弱一级,若A市所受风力不到4级,则称不受台风影响,根据以上信息回答下列问题:
(1)A市是否会受到这次台风影响?说明理由;
(2)若A市受到影响,所受最大风力是几级?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
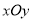 中,点
中,点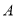 坐标为
坐标为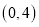 ,点
,点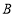 坐标为
坐标为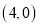 ,过点
,过点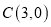 作直线
作直线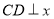 轴,垂足为
轴,垂足为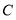 ,交线段
,交线段 于点
于点 .
.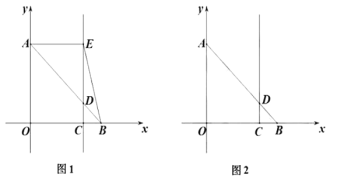
(1)如图1,过点
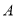 作
作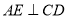 ,垂足为
,垂足为 ,连接
,连接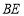 .
.①填空:
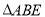 的面积为______;②点
的面积为______;②点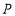 为直线
为直线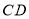 上一动点,当
上一动点,当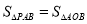 时,求点
时,求点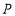 的坐标;
的坐标;(2)如图2,点
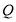 为线段
为线段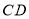 延长线上一点,连接
延长线上一点,连接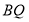 ,
,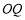 ,线段
,线段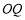 交
交 于点
于点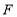 ,若
,若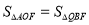 ,请直接写出点
,请直接写出点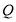 的坐标为______.
的坐标为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
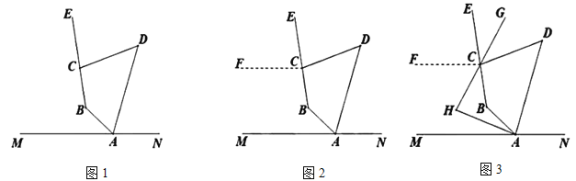
如图1,点
 是直线
是直线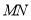 上一点,
上一点,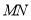 上方的四边形
上方的四边形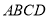 中,
中,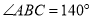 ,延长
,延长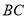 ,
,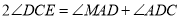 ,探究
,探究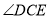 与
与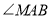 的数量关系,并证明.
的数量关系,并证明.小白的想法是:“作
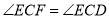 (如图2),通过推理可以得到
(如图2),通过推理可以得到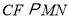 ,从而得出结论”.
,从而得出结论”.请按照小白的想法完成解答:
拓展延伸:
保留原题条件不变,
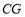 平分
平分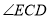 ,反向延长
,反向延长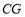 ,交
,交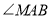 的平分线于点
的平分线于点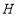 (如图3),设
(如图3),设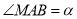 ,请直接写出
,请直接写出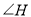 的度数(用含
的度数(用含 的式子表示).
的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2-4x+3与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上.则平移后的抛物线解析式为 ( )
A. y=x2+2x+1 B. y=x2+2x-1 C. y=x2-2x+1 D. y=x2-2x-1
相关试题

