【题目】在平面直角坐标系![]() 中,点
中,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,垂足为
轴,垂足为![]() ,交线段
,交线段![]() 于点
于点![]() .
.
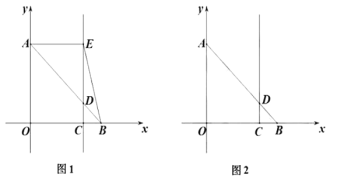
(1)如图1,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
①填空:![]() 的面积为______;②点
的面积为______;②点![]() 为直线
为直线![]() 上一动点,当
上一动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,点![]() 为线段
为线段![]() 延长线上一点,连接
延长线上一点,连接![]() ,
,![]() ,线段
,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,请直接写出点
,请直接写出点![]() 的坐标为______.
的坐标为______.
参考答案:
【答案】(1)①6;②![]() 的坐标为
的坐标为![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)①易证四边形AECO为矩形,则点B到AE的距离为OA,AE=OC=3,OA=CE=4,S△ABE=![]() AEOA,即可得出结果;
AEOA,即可得出结果;
②设点![]() 的坐标为
的坐标为![]() ,分两种情况: 点
,分两种情况: 点![]() 在点
在点![]() 上方,连接
上方,连接![]() ,得
,得![]() =
=![]() +
+![]() +
+![]() =8,点
=8,点![]() 在点
在点![]() 的下方,得
的下方,得![]() =8,分别列出方程解方程即可得出结果;
=8,分别列出方程解方程即可得出结果;
(2)由S△AOF=S△QBF,则S△AOB=S△QOB,△AOB与△QOB是以AB为同底的三角形,高分别为:OA、QC,得出OA=CQ,即可得出结果.
解:(1)①∵CD⊥x轴,AE⊥CD,
∴AE∥x轴,四边形AECO为矩形,点B到AE的距离为OA,
∵点A(0,4),点C(3,0),
∴AE=OC=3,OA=CE=4,
∴S△ABE=![]() AEOA=
AEOA=![]() ×3×4=6,
×3×4=6,
故答案为:6;
②设点![]() 的坐标为
的坐标为![]() .
.
(i)∵点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴点![]() 在点
在点![]() 上方,连接
上方,连接![]() (如图1).根据题意得
(如图1).根据题意得

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴当点![]() 的坐标为
的坐标为![]() .
.
(ii)点![]() 在点
在点![]() 的下方,连接
的下方,连接![]() (如图2).
(如图2).
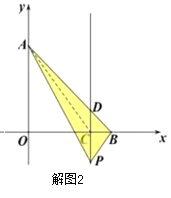
∵![]() .
.
∴![]() .
.
∴点![]() 在点
在点![]() 的下方,根据题意得
的下方,根据题意得
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴当点![]() 的坐标为
的坐标为![]() .
.
(2)(2)∵S△AOF=S△QBF,如图3所示:
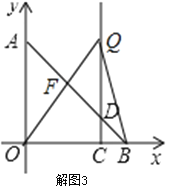
∴S△AOB=S△QOB,
∵△AOB与△QOB是以AB为同底的三角形,高分别为:OA、QC,
∴OA=CQ,
∴点Q的坐标为(3,4),
故答案为:(3,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市进行“新城区改造建设”,有甲、乙两种车参加运土,已知5辆甲种车和2辆乙种车一次共可运土64米
 ,3辆甲种车和1辆乙种车一次共可运土36米
,3辆甲种车和1辆乙种车一次共可运土36米 .
.(1)求甲、乙两种车每辆一次可分别运土多少米
 ;
;(2)某公司派甲、乙两种汽车共10辆参加运土,且一次运土总量不低于100米
 ,求公司最多要派多少辆甲种汽车参加运土.
,求公司最多要派多少辆甲种汽车参加运土. -
科目: 来源: 题型:
查看答案和解析>>【题目】台风是一种自然灾害,如图,气象部门观测到距离A市正北方向200千米的B处有一台风中心,其中心最大风力为12级,该台风中心正以18千米/时的速度沿直线向C移动,且台风中心风力不变,已知每远离台风中心20千米,风力就减弱一级,若A市所受风力不到4级,则称不受台风影响,根据以上信息回答下列问题:
(1)A市是否会受到这次台风影响?说明理由;
(2)若A市受到影响,所受最大风力是几级?
-
科目: 来源: 题型:
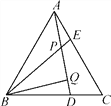
查看答案和解析>>【题目】如图,等边△ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q.
(1)求证:BP=2PQ;
(2)若PE=1,PQ=3,试求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
如图1,点
 是直线
是直线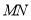 上一点,
上一点,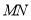 上方的四边形
上方的四边形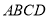 中,
中,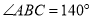 ,延长
,延长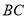 ,
,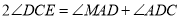 ,探究
,探究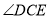 与
与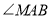 的数量关系,并证明.
的数量关系,并证明.小白的想法是:“作
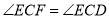 (如图2),通过推理可以得到
(如图2),通过推理可以得到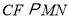 ,从而得出结论”.
,从而得出结论”.请按照小白的想法完成解答:
拓展延伸:
保留原题条件不变,
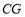 平分
平分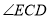 ,反向延长
,反向延长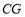 ,交
,交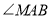 的平分线于点
的平分线于点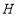 (如图3),设
(如图3),设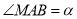 ,请直接写出
,请直接写出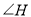 的度数(用含
的度数(用含 的式子表示).
的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2-4x+3与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上.则平移后的抛物线解析式为 ( )
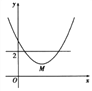
A. y=x2+2x+1 B. y=x2+2x-1 C. y=x2-2x+1 D. y=x2-2x-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子的长度为25米,斜靠在墙上,梯子低部离墙底端为7米.
(1)这个梯子顶端离地面有 米;
(2)如果梯子的顶端下滑了4米,那么梯子的底部在水平方向滑动了几米?

相关试题

